Cho tứ diện đều có chiều cao bằng h Thể tích của khối t
Câu hỏi
Nhận biếtCho tứ diện đều có chiều cao bằng h. Thể tích của khối tứ diện đã cho là:
Đáp án đúng: B
Lời giải của Tự Học 365
Phương pháp giải:
- Gọi tứ diện đều ABCD cạnh a, sử dụng tính chất tam giác đều và định lí Pytago tính a theo h.
- Sử dụng công thức tính thể tích khối chóp có đường cao h, diện tích đáy B là \(V = \dfrac{1}{3}Bh\).
Giải chi tiết:
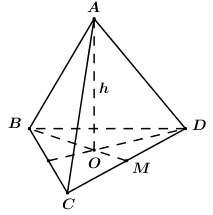
Gọi tứ diện đều ABCD cạnh a, O là trọng tâm tam giác dều BCD \( \Rightarrow AO \bot \left( {BCD} \right)\).
Gọi M là trung điểm của CD. Tam giác BCD đều cạnh a \( \Rightarrow BM = \dfrac{{a\sqrt 3 }}{2}\) \( \Rightarrow BO = \dfrac{2}{3}BM = \dfrac{{a\sqrt 3 }}{3}\).
Áp dụng định lí Pytago trong tam giác vuông ABO ta có:
\(\begin{array}{l}A{B^2} = B{O^2} + A{O^2}\\ \Leftrightarrow {a^2} = \dfrac{{{a^2}}}{3} + {h^2}\\ \Leftrightarrow \dfrac{{2{a^2}}}{3} = {h^2}\\ \Leftrightarrow {a^2} = \dfrac{{3{h^2}}}{2}\end{array}\)
\( \Rightarrow {S_{\Delta BCD}} = \dfrac{{{a^2}\sqrt 3 }}{4} = \dfrac{{3{h^2}}}{2}.\dfrac{{\sqrt 3 }}{4} = \dfrac{{3\sqrt 3 {h^2}}}{8}\).
Vậy \({V_{ABCD}} = \dfrac{1}{3}AO.{S_{\Delta BCD}} = \dfrac{1}{3}.h.\dfrac{{3\sqrt 3 {h^2}}}{8} = \dfrac{{\sqrt 3 {h^3}}}{8}.\)
Chọn B.
Luyện tập
Câu hỏi liên quan
-
Người Cam-pu-chia đã sáng tạo ra chữ viết vào thời gian nào?
-
Kinh đô của nước ta dưới thời Ngô là
-
Em hãy trình bày sự hình thành và phát triển của các vương quốc phong kiến Đông Nam Á từ nửa sau thế kỷ X đến đầu thế kỷ XVI?
-
Công trình kiến trúc tiêu biểu của vương quốc Cam-pu-chia thời phong kiến là
-
Quốc hiệu của nước ta dưới thời Đinh – Tiền Lê là
-
Pha Ngừm đã thành lập nước Lan Xang vào năm nào?
-
Bằng kiến thức đã học về cuộc kháng chiến chống quân xâm lược Tống (1075 - 1077), em hãy:
a. Chỉ ra những nét độc đáo trong cách đánh giặc của Lý Thường Kiệt?
b. Đánh giá vai trò của Lý Thường Kiệt trong cuộc kháng chiến?
-
Người chỉ huy đoàn tham hiểm lần đầu tiên đi vòng quanh trái đất bằng đường biển là
-
Quê hương của phong trào văn hóa Phục hưng là
-
Công trình kiến trúc tiêu biểu của vương quốc Lào thời phong kiến là