Cho tam giác ABC nhọn AB lt AC nội tiếp đường tròn tâm

Câu hỏi
Nhận biếtĐáp án đúng:
Lời giải của Tự Học 365
Phương pháp giải:
a) Sử dụng tam giác đồng dạng, tứ giác nội tiếp để bắc cầu góc
b) Vận dụng định lý Ta – lét và tính chất đường phân giác trong, phân giác ngoài của tam giác
c) Ta sẽ chứng minh H là trực tâm tam giác AKM thông qua các bổ đề quen thuộc
Giải chi tiết:
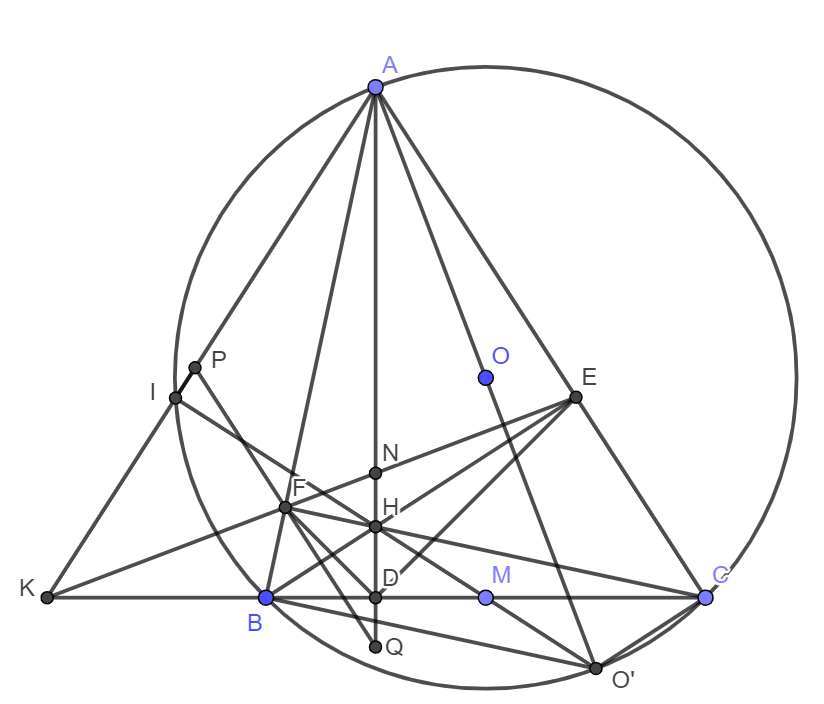
a) Tứ giác BFEC nội tiếp và ΔKBF∼ΔKEC
Khi đó KFKC=KBKE⇒KB.KC=KE.KF
Tứ giác BDHF nội tiếp , suy ra \widehat {FBH} = \widehat {FDH} & (1)
Tứ giác CDHE nội tiếp, suy ra \widehat {HDE} = \widehat {HCE} & (2)
Ta có: ^FBE=^FCE(3)(tứ giác BFEC nội tiếp)
Từ (1),(2),(3)⇒^FDH=^EDH⇒HD là phân giác của \widehat {FDE} & (4)
Chứng minh tương tự, ta được:HE là phân giác của ^FED(5)
Từ (4) và (5) ⇒H là tâm đường tròn nội tiếp ΔDEF
b) Gọi N là giao điểm của AD,KE
Theo tính chất đường phân giác trong của ΔDEF⇒NFNE=DFDE(6)
Ta có KD là phân giác ngoài của ΔFDE tại đỉnh D. Theo tính chất đường phân giác ngoài của ΔDEF⇒KFKE=DFDE(7)
Từ (6) và(7) ⇒NFNE=KFKE(8)
Vì PQ//AC, theo định lý Ta – let ta có:
NFNE=FQAEvà KFKE=FPAE(9)
Từ (8) và (9) ⇒FQAE=FPAE⇒FQ=FP
c) Gọi I là giao điểm của KA với đường tròn (O)(I khác A) và A′ là điểm đối xứng với A qua O. Chứng minh được BHCA′ là hình bình hành (bổ đề quen thuộc)
Suy ra ba điểm H,M,A′ thẳng hàng
Vì tứ giác AIBC nội tiếp đường tròn (O)⇒KI.KA=KB.KC
Theo câu 1) thì KB.KC=KF.KE
Suy ra KI.KA=KF.KE⇒AIFE là tứ giác nội tiếp
Vì ba điểm A,E,F thuộc đường tròn đường kính AH⇒I thuộc đường tròn đường kính AH⇒AI⊥HI
Ta có ^AIA′=900⇒AI⊥A′I
Kết hợp với AI⊥HI⇒H,I,A′ thẳng hàng
Mặt khác ba điểm H,M,A′ thẳng hàng nên 4 điểm H,M,I,A′ thẳng hàng
Xét ΔAKMcó AH⊥KMvà MH⊥AK⇒Hlà trực tâm ΔAKM
Suy ra KH⊥AM
Luyện tập
Câu hỏi liên quan
-

Công trình kiến trúc tiêu biểu của vương quốc Lào thời phong kiến là
-

Công trình kiến trúc tiêu biểu của vương quốc Cam-pu-chia thời phong kiến là
-

Người chỉ huy đoàn tham hiểm lần đầu tiên đi vòng quanh trái đất bằng đường biển là
-

Em hãy trình bày sự hình thành và phát triển của các vương quốc phong kiến Đông Nam Á từ nửa sau thế kỷ X đến đầu thế kỷ XVI?
-

Kinh đô của nước ta dưới thời Ngô là
-

Người Cam-pu-chia đã sáng tạo ra chữ viết vào thời gian nào?
-

Bằng kiến thức đã học về cuộc kháng chiến chống quân xâm lược Tống (1075 - 1077), em hãy:
a. Chỉ ra những nét độc đáo trong cách đánh giặc của Lý Thường Kiệt?
b. Đánh giá vai trò của Lý Thường Kiệt trong cuộc kháng chiến?
-

Quốc hiệu của nước ta dưới thời Đinh – Tiền Lê là
-

Quê hương của phong trào văn hóa Phục hưng là
-

Pha Ngừm đã thành lập nước Lan Xang vào năm nào?

