Cho hình hộp ABCDA’B’C’D’ tâm O Một mặt phằng α đi qua

Câu hỏi
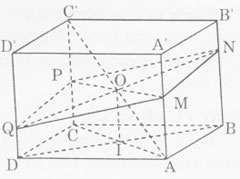
Nhận biếtCho hình hộp ABCD.A’B’C’D’ tâm O. Một mặt phằng (α) đi qua O cắt các cạnh AA’, BB’, CC’, DD’ lần lượt tại các điểm M, N, P, Q. Ta xét các mệnh đề sau:
1. Tứ giác MNPQ là một hình bình hành.
2. Điếm O là trung điểm của cả hai đoạn thẳng MP và NQ.
3. Tổng AM + CP có giá trị không đổi.
4. Tổng BN + DQ có giá trị không đối.
Trong các mệnh đề trên:
Đáp án đúng: D
Lời giải của Tự Học 365
Ta có: (ABB'A') // (DCC'D'); (α) cắt hai mặt phẳng này theo các giao tuyến MN và QP nên MN // QP.
Tương tự: MQ // NP. Do đó MNPQ là một hình bình hành.
O chính là giao điểm của hai đường chéo MP và NQ, nên O là trung điếm của MP và NQ.
Tứ giác ACPM là hình thang, IO là đường trung bình nên:
AM + CP = 2IO (hằng số)
Tương tự: BN + DQ = 2OI
Ta thấy cả bốn mệnh đề đều đúng.
Luyện tập
Câu hỏi liên quan
-

Công trình kiến trúc tiêu biểu của vương quốc Cam-pu-chia thời phong kiến là
-

Công trình kiến trúc tiêu biểu của vương quốc Lào thời phong kiến là
-

Quốc hiệu của nước ta dưới thời Đinh – Tiền Lê là
-

Bằng kiến thức đã học về cuộc kháng chiến chống quân xâm lược Tống (1075 - 1077), em hãy:
a. Chỉ ra những nét độc đáo trong cách đánh giặc của Lý Thường Kiệt?
b. Đánh giá vai trò của Lý Thường Kiệt trong cuộc kháng chiến?
-

Người chỉ huy đoàn tham hiểm lần đầu tiên đi vòng quanh trái đất bằng đường biển là
-

Quê hương của phong trào văn hóa Phục hưng là
-

Em hãy trình bày sự hình thành và phát triển của các vương quốc phong kiến Đông Nam Á từ nửa sau thế kỷ X đến đầu thế kỷ XVI?
-

Pha Ngừm đã thành lập nước Lan Xang vào năm nào?
-

Người Cam-pu-chia đã sáng tạo ra chữ viết vào thời gian nào?
-

Kinh đô của nước ta dưới thời Ngô là
