Cho hàm số f x = ax^3 + bx^2 + cx + d abcd in mathbb
Câu hỏi
Nhận biếtCho hàm số \\(f\\left( x \\right) = a{x^3} + b{x^2} + cx + d\\) \\(\\left( {a,b,c,d \\in \\mathbb{R}} \\right)\\) có bảng biến thiên như sau:
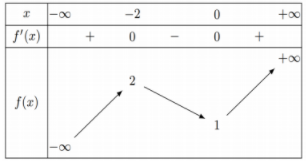
Có bao nhiêu số dương trong các số \\(a,b,c,d\\)?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Dựa vào BBT ta thấy \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = + \infty \Rightarrow a > 0\).
Ta có \(f\left( 0 \right) = 1 \Rightarrow d = 1 > 0\).
Ta có: \(y' = 3a{x^2} + 2bx + c\), hàm số có 2 điểm cực trị \({x_1} = 0;{x_2} = - 2\)
\( \Rightarrow y'\left( 0 \right) = 0 \Rightarrow c = 0\)
Ta có \({x_1} + {x_2} = - \dfrac{{2b}}{{3a}} < 0\), mà \(a > 0 \Rightarrow b > 0\).
Vậy có 3 số dương là \(a,b,d\).
Chọn D.
Luyện tập
Câu hỏi liên quan
-
Người chỉ huy đoàn tham hiểm lần đầu tiên đi vòng quanh trái đất bằng đường biển là
-
Quê hương của phong trào văn hóa Phục hưng là
-
Công trình kiến trúc tiêu biểu của vương quốc Cam-pu-chia thời phong kiến là
-
Pha Ngừm đã thành lập nước Lan Xang vào năm nào?
-
Công trình kiến trúc tiêu biểu của vương quốc Lào thời phong kiến là
-
Em hãy trình bày sự hình thành và phát triển của các vương quốc phong kiến Đông Nam Á từ nửa sau thế kỷ X đến đầu thế kỷ XVI?
-
Người Cam-pu-chia đã sáng tạo ra chữ viết vào thời gian nào?
-
Bằng kiến thức đã học về cuộc kháng chiến chống quân xâm lược Tống (1075 - 1077), em hãy:
a. Chỉ ra những nét độc đáo trong cách đánh giặc của Lý Thường Kiệt?
b. Đánh giá vai trò của Lý Thường Kiệt trong cuộc kháng chiến?
-
Quốc hiệu của nước ta dưới thời Đinh – Tiền Lê là
-
Kinh đô của nước ta dưới thời Ngô là