Cho hai góc angle AOx và angle BOx không kề nhaua Nếu a
Câu hỏi
Nhận biếtĐáp án đúng:
Lời giải của Tự Học 365
Phương pháp giải:
+ Nếu tia \(Oz\) là tia phân giác của \(\angle xOy\) thì \(\angle xOz = \angle yOz = \dfrac{1}{2}\angle xOy\)
+ Xét ba trường hợp là \(a < b;a > b;a = b\)
Giải chi tiết:
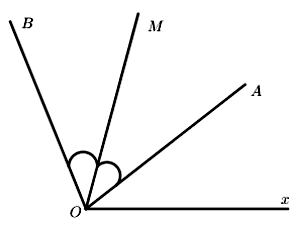
a) Ta có: \(\angle AOx + \angle AOB = \angle BOx\)
\(38^\circ + \angle AOB = 112^\circ \)
\( \Rightarrow \angle AOB = 112^\circ - 38^\circ = 74^\circ \)
b) + Nếu \(a = b \Rightarrow \angle AOx = \angle BOx \Rightarrow OA\) và \(OB\) là hai tia trùng nhau
\( \Rightarrow \angle AOB = 0^\circ \) và không tồn tại tia \(OM\)
+ Nếu \(a > b \Rightarrow \angle AOx > \angle BOx \Rightarrow OB\) nằm giữa hai tia \(Ox\) và \(OA\)
Ta có: \(\angle AOB = \angle AOx - \angle BOx = a - b\)
Vì tia \(OM\) là tia phân giác của \(\angle AOB\) nên \(\angle AOM = \angle BOM = \dfrac{1}{2}\angle AOB = \dfrac{{a - b}}{2}\)
Lại có: \(\angle MOx = \angle BOx + \angle MOB = b + \dfrac{{a - b}}{2} = \dfrac{{a + b}}{2}\)
+ Nếu \(a < b \Rightarrow \angle AOx < \angle BOx \Rightarrow OA\) nằm giữa hai tia \(Ox\) và \(OB\)
Ta có: \(\angle AOB = \angle BOx - \angle AOx = b - a\)
Vì \(OM\) là tia phân giác của \(\angle AOB\) nên \(\angle AOM = \angle MOB = \dfrac{1}{2}\angle AOB = \dfrac{{b - a}}{2}\)
Lại có: \(\angle MOx = \angle MOA + \angle AOx = \dfrac{{b - a}}{2} + a = \dfrac{{a + b}}{2}\)
Luyện tập
Câu hỏi liên quan
-
Người Cam-pu-chia đã sáng tạo ra chữ viết vào thời gian nào?
-
Quê hương của phong trào văn hóa Phục hưng là
-
Công trình kiến trúc tiêu biểu của vương quốc Cam-pu-chia thời phong kiến là
-
Bằng kiến thức đã học về cuộc kháng chiến chống quân xâm lược Tống (1075 - 1077), em hãy:
a. Chỉ ra những nét độc đáo trong cách đánh giặc của Lý Thường Kiệt?
b. Đánh giá vai trò của Lý Thường Kiệt trong cuộc kháng chiến?
-
Pha Ngừm đã thành lập nước Lan Xang vào năm nào?
-
Em hãy trình bày sự hình thành và phát triển của các vương quốc phong kiến Đông Nam Á từ nửa sau thế kỷ X đến đầu thế kỷ XVI?
-
Công trình kiến trúc tiêu biểu của vương quốc Lào thời phong kiến là
-
Quốc hiệu của nước ta dưới thời Đinh – Tiền Lê là
-
Người chỉ huy đoàn tham hiểm lần đầu tiên đi vòng quanh trái đất bằng đường biển là
-
Kinh đô của nước ta dưới thời Ngô là