08 diểm Ông An dự định làm bánh chưng và bánh tét để

Câu hỏi
Nhận biết( 0,8 diểm ) Ông An dự định làm bánh chưng và bánh tét để bán vào dịp Tết Quý Mão 2023 với giá lần lượt là 130 nghìn và 160 nghìn đồng mỗi chiếc. Biết rằng để làm một chiếc bánh chưng cần (500{rm{;g}}) gạo nếp và (150{rm{;g}}) thịt, để làm một chiếc bánh tét cần (400{rm{;g}}) gạo nếp và (200{rm{;g}}) thịt. Tính số lượng bánh mỗi loại để số tiền bán bánh thu được là lớn nhất, biết rằng ông An chỉ sử dụng tối đa (10{rm{;kg}}) nếp và (4,2{rm{;kg}}) thịt.
Đáp án đúng:
Lời giải của Tự Học 365
Lập hệ phương trình bậc nhất 2 ẩn, biểu diễn miền nghiệm trên mặt phẳng tọa độ, xác định các đỉnh và tính giá trị số tiền lớn nhất.
Giải chi tiết:
Gọi $x, y$ (cái) lần lượt là số bánh chưng và bánh tét mà ông An làm. Điều kiện: \(x,y \in \mathbb{N}\).
Ta có hệ bất phương trình:
\(\left\{ {\begin{array}{*{20}{l}}{x \ge 0}\{y \ge 0}\{500x + 400y \le 10000}\{150x + 200y \le 4200}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{x \ge 0}\{y \ge 0}\{5x + 4y \le 100}\{3x + 4y \le 84}\end{array}} \right.} \right.\)
Vẽ các đường thẳng \(x = 0,y = 0,5x + 4y = 100\), \(3x + 4y = 84\) trên mặt phẳng tọa độ và xác định được miền nghiệm của hệ bất phương trình như hình vẽ (miền đa giác màu trắng):
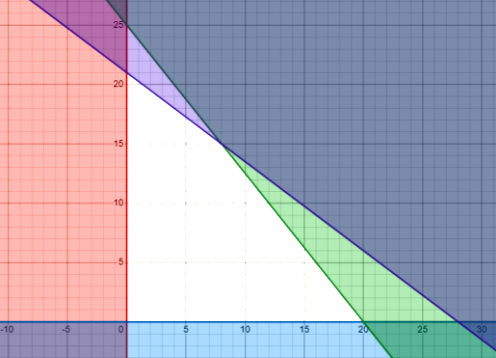
Các giá trị của \(F\) tại các đỉnh của đa giác số tiền bán bánh \(F = 130x + 160y\) (nghìn đồng) là:
Tại \((0;0):F = 0\).
Tại \((0;21):F = 3360\).
Tại \((20;0):F = 2600\).
Tại \((8;15):F = 3440\).
Vậy \(F\) lớn nhất khi \(x = 8\) và \(y = 15\).
Luyện tập
Câu hỏi liên quan
-

Quốc hiệu của nước ta dưới thời Đinh – Tiền Lê là
-

Em hãy trình bày sự hình thành và phát triển của các vương quốc phong kiến Đông Nam Á từ nửa sau thế kỷ X đến đầu thế kỷ XVI?
-

Người chỉ huy đoàn tham hiểm lần đầu tiên đi vòng quanh trái đất bằng đường biển là
-

Bằng kiến thức đã học về cuộc kháng chiến chống quân xâm lược Tống (1075 - 1077), em hãy:
a. Chỉ ra những nét độc đáo trong cách đánh giặc của Lý Thường Kiệt?
b. Đánh giá vai trò của Lý Thường Kiệt trong cuộc kháng chiến?
-

Pha Ngừm đã thành lập nước Lan Xang vào năm nào?
-

Quê hương của phong trào văn hóa Phục hưng là
-

Người Cam-pu-chia đã sáng tạo ra chữ viết vào thời gian nào?
-

Kinh đô của nước ta dưới thời Ngô là
-

Công trình kiến trúc tiêu biểu của vương quốc Cam-pu-chia thời phong kiến là
-

Công trình kiến trúc tiêu biểu của vương quốc Lào thời phong kiến là
