Cho nửa đường tròn tâm O với bán kính R đường kính AB T

Câu hỏi
Nhận biếtĐáp án đúng:
Lời giải của Tự Học 365
Phương pháp giải:
a) Chứng minh ΔMAO=ΔMEO(c.c.c)⇒∠MAO=∠MEO mà ∠MAB=900 suy ra ∠MEO=900
Do đó ME là tiếp tuyến của đường tròn (O).
b) Chứng minh MI là phân giác của ∠AME và AI là phân giác của ∠MAE suy ra I là tâm đường tròn nội tiếp ΔAME.
c) Chứng minh ΔMOP vuông tại O
Tính được SΔOMP=12OE.MP
Vận dụng bất đẳng thức Cô – si để tìm giá trị nhot nhất
d) Gọi F là giao điểm của QD,AB và G là giao điểm của AE,BP
Chứng minh PG=PB và MA=MC
Chứng minh D là trung điểm của QF
Chứng minh ∠DAF=∠PAB⇒A,D,P thẳng hàng
Giải chi tiết:
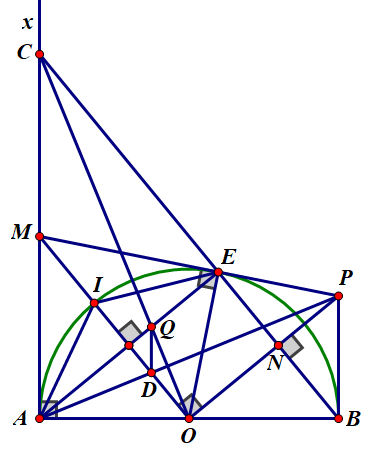
a) Do E đối xứng với A qua OM nên MA=ME;OA=OE
Xét ΔMAO và ΔMEO có:
MA=ME(cmt)OA=OE(cmt)MOchung}⇒ΔMAO=ΔMEO(c.c.c)⇒∠MAO=∠MEO (1) (hai góc tương ứng)
Ax là tiếp tuyến của đường tròn (O)⇒Ax⊥AB⇒∠MAB=900 hay ∠MAO=900 (2)
Từ (1) và (2), suy ra ∠MEO=900 mà E∈(O)
Do đó ME là tiếp tuyến của đường tròn (O).
b) AM,EM là tiếp tuyến của đường tròn (O)⇒MI là phân giác của ∠AME (3) (tính chất hai tiếp tuyến cắt nhau)
Ta có: A,E đối xứng với nhau qua OM⇒OM là đường trung trực của đoạn AE
Mà I∈OM⇒IA=IE (tính chất đường trung trực của đoạn thẳng)
Lại có: MA là tiếp tuyến của (O)
⇒∠MAI=∠IEA=∠IAE
⇒AI là phân giác của ∠MAE (4)
Từ (3) và (4), suy ra I là tâm đường tròn nội tiếp ΔAME.
c) Ta có: OE=OB (bán kính đường tròn (O))⇒ΔOBE cân tại O
mà N là trung điểm của BE⇒ON⊥BE⇒OP⊥BE (vì O,N,P thẳng hàng)
Ta có: E∈(O)⇒∠AEB=900⇒AE⊥EB
Ta có: {BE⊥OPBE⊥AE⇒OP//AE (quan hệ từ vuông góc đến song song)
MO là đường trung trực của đoạn AE⇒MO⊥AE
Ta có: {OP//AEMO⊥AE⇒MO⊥OP (quan hệ từ vuông góc đến song song)
⇒∠MOP=900 nên ΔMOP vuông tại O
ΔMOP vuông tại O có OE⊥MP (do ME là tiếp tuyến của đường tròn (O))
⇒MP.EP=OE2=R2 (hệ thức lượng trong tam giác vuông)
⇒SΔOMP=12OE.MP=12R.(ME+EP)≥12R.2√ME.EP=12R.2R=R2
Dấu “=” xảy ra khi ME=EP=R⇒ΔMEO vuông cân tại E⇒OM=R√2=OA√2⇒MA=R
d) Gọi F là giao điểm của QD,AB
G là giao điểm của AE,BP
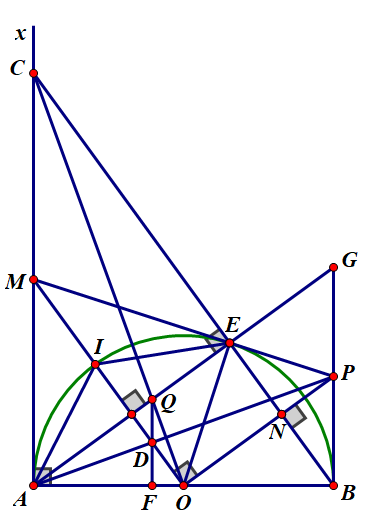
Ta có: OP//AE(⊥BE),O là trung điểm của AB
⇒OP là đường trung bình của tam giác ABG
⇒P là trung điềm của BG
⇒PG=PB
Ta có: C là giao điểm của BE,AM
Chứng minh tương tự, ta có được M là trung điểm của AC⇒MA=MC
Lại có: QF//AC
⇒QDMC=ODOM=DFMA⇒QD=DF
⇒D là trung điểm của QF
Ta có: QF//BG(⊥AB)
AFAB=QFGB=2DF2BP=DFBF
Lại có: ∠AFD=∠ABP(=900)
⇒A,D,P thẳng hàng
Luyện tập
Câu hỏi liên quan
-

Pha Ngừm đã thành lập nước Lan Xang vào năm nào?
-

Em hãy trình bày sự hình thành và phát triển của các vương quốc phong kiến Đông Nam Á từ nửa sau thế kỷ X đến đầu thế kỷ XVI?
-

Người chỉ huy đoàn tham hiểm lần đầu tiên đi vòng quanh trái đất bằng đường biển là
-

Bằng kiến thức đã học về cuộc kháng chiến chống quân xâm lược Tống (1075 - 1077), em hãy:
a. Chỉ ra những nét độc đáo trong cách đánh giặc của Lý Thường Kiệt?
b. Đánh giá vai trò của Lý Thường Kiệt trong cuộc kháng chiến?
-

Công trình kiến trúc tiêu biểu của vương quốc Cam-pu-chia thời phong kiến là
-

Kinh đô của nước ta dưới thời Ngô là
-

Công trình kiến trúc tiêu biểu của vương quốc Lào thời phong kiến là
-

Quốc hiệu của nước ta dưới thời Đinh – Tiền Lê là
-

Người Cam-pu-chia đã sáng tạo ra chữ viết vào thời gian nào?
-

Quê hương của phong trào văn hóa Phục hưng là

