Cho mạch dao động LC gồm có nguồn điện có suất điện độn
Câu hỏi
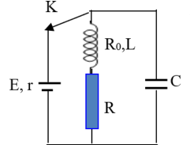
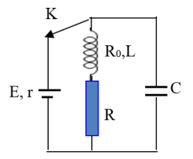
Nhận biếtCho mạch dao động \\(LC\\) gồm có nguồn điện có suất điện động \\(E = 12\\,\\,V\\), điện trở trong \\(r = 1\\,\\,\\Omega \\), tụ có điện dung \\(C = 200\\,\\,\\mu F\\), cuộn dây có hệ số tự cảm \\(L = 0,2\\,\\,H\\) và điện trở là \\({R_0} = 4\\,\\,\\Omega \\); điện trở \\(R = 20\\,\\,\\Omega \\). Ban đầu \\(K\\) đóng, khi trạng thái trong mạch đã ổn định người ta ngắt khoá \\(K\\). Tính nhiệt lượng tỏa ra trên điện trở \\(R\\) trong thời gian từ khi ngắt \\(K\\) đến khi dao động trong mạch tắt hoàn toàn?
Đáp án đúng: B
Lời giải của Tự Học 365
Phương pháp giải:
Dòng điện một chiều không đi qua tụ điện, cuộn dây đóng vai trò như dây dẫn
Định luật Ôm cho dòng điện một chiều: \(I = \dfrac{E}{{R + {R_0} + r}}\)
Hiệu điện thế: \(U = I.\left( {R + {R_0}} \right)\)
Năng lượng điện từ: \(W = \dfrac{{C{U^2}}}{2} + \dfrac{{L{I^2}}}{2}\)
Nhiệt lượng tỏa ra trên điện trở: \(Q = {I^2}Rt\)
Giải chi tiết:
Khi đóng khóa K, dòng điện một chiều chỉ đi qua cuộn dây mà không qua tụ điện
Cường độ dòng điện qua cuộn dây là:
\(I = \dfrac{E}{{R + {R_0} + r}} = \dfrac{{12}}{{20 + 4 + 1}} = 0,48\,\,\left( A \right)\)
Hiệu điện thế giữa hai đầu tụ điện (mạch ngoài) là:
\(U = I\left( {R + {R_0}} \right) = 0,48.\left( {20 + 4} \right) = 11,52\,\,\left( V \right)\)
Năng lượng điện từ của mạch dao động là:
\({\rm{W}} = \dfrac{{C{U^2}}}{2} + \dfrac{{L{I^2}}}{2} = \dfrac{{{{200.10}^{ - 6}}.11,{{52}^2}}}{2} + \dfrac{{0,2.0,{{48}^2}}}{2} = 0,036311\,\,\left( J \right)\)
Nhiệt lượng tỏa ra trên cuộn dây và trên điện trở R là:
\(\left\{ \begin{array}{l}{Q_{{R_0}}} = {I^2}{R_0}t\\{Q_R} = {I^2}Rt\end{array} \right. \Rightarrow \dfrac{{{Q_{{R_0}}}}}{{{Q_R}}} = \dfrac{{{R_0}}}{R} = \dfrac{4}{{20}} = \dfrac{1}{5} \Rightarrow {Q_{{R_0}}} = \dfrac{1}{5}{Q_R}\)
Lại có: \({Q_{{R_0}}} + {Q_R} = {\rm{W}} \Rightarrow \dfrac{6}{5}{Q_R} = 0,036311\,\,\left( J \right)\)
\( \Rightarrow {Q_R} \approx 0,03026\,\,\left( J \right) = 30,26\,\,\left( {mJ} \right)\)
Chọn B.
Luyện tập
Câu hỏi liên quan
-

Người Cam-pu-chia đã sáng tạo ra chữ viết vào thời gian nào?
-

Quốc hiệu của nước ta dưới thời Đinh – Tiền Lê là
-

Kinh đô của nước ta dưới thời Ngô là
-

Người chỉ huy đoàn tham hiểm lần đầu tiên đi vòng quanh trái đất bằng đường biển là
-

Công trình kiến trúc tiêu biểu của vương quốc Cam-pu-chia thời phong kiến là
-

Em hãy trình bày sự hình thành và phát triển của các vương quốc phong kiến Đông Nam Á từ nửa sau thế kỷ X đến đầu thế kỷ XVI?
-

Bằng kiến thức đã học về cuộc kháng chiến chống quân xâm lược Tống (1075 - 1077), em hãy:
a. Chỉ ra những nét độc đáo trong cách đánh giặc của Lý Thường Kiệt?
b. Đánh giá vai trò của Lý Thường Kiệt trong cuộc kháng chiến?
-

Pha Ngừm đã thành lập nước Lan Xang vào năm nào?
-

Quê hương của phong trào văn hóa Phục hưng là
-

Công trình kiến trúc tiêu biểu của vương quốc Lào thời phong kiến là
