Cho sơ đồ phả hệ sau: <

Câu hỏi
Nhận biếtCho sơ đồ phả hệ sau:
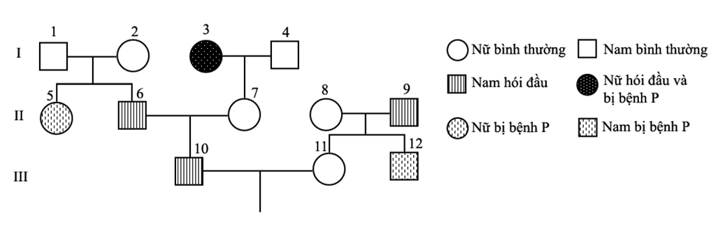
Biết rằng hai cặp gen qui định hai tính trạng nói trên không cùng nằm trong một nhóm gen liên kết: bệnh hói đầu do alen trội H nằm trên NST thường qui định, kiểu gen dị hợp Hh biểu hiện hói đầu ở người nam và không hói đầu ở người nữ và quần thể này ở trạng thái cân bằng và có tỉ lệ người bị hói đầu là 20%.
I. Có tối đa 5 người có kiểu gen đồng hợp về tính trạng hói đầu.
II. Xác định được chính xác kiểu gen của 7 người về cả hai bệnh.
III. Khả năng người số 10 mang ít nhất 1 alen lặn là 13/15.
IV. Xác suất để đứa con đầu lòng của cặp vợ chồng số 10 và 11 là con gái, không hói đầu và không mang
alen gây bệnh P là 21/110.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
- Bệnh hói đầu:
+ Ở nam: HH + Hh: hói; hh: không hói.
+ Ở nữ: HH: hói; Hh + hh: không hói.
+ p2HH + 2pqHh + q2hh = 1.
\(\left\{ \begin{array}{l}{p^2} + pq = 0,2\\p + q = 1\end{array} \right.\) → p = 0,2; q = 0,8.
+ CBDT: 0,04HH + 0,32Hh + 0,64hh = 1.
- Bố (1) và mẹ (2) không mắc bệnh P để con gái (5) mắc bệnh P → bệnh P do gen lặn nằm trên NST thường quy định.

(I) sai: Có tối đa 8 người có kiểu gen đồng hợp về tính trạng hói đầu: 1,3,4,5,8,10,11,12.
Chú ý: Người số 2 bắt buộc phải Hh thì mới sinh được người con thứ (6) Hh.
(II) Sai: Chỉ có 6 người biết chính xác kiểu gen về cả 2 bệnh: 1,2,3,7, 9,12.
(III) Đúng: Người số 10 mang ít nhất 1 alen lặn = 1 – AAHH =\(1 - \frac{2}{5} \times \frac{1}{3} = \frac{{13}}{{15}}\)
(IV) Đúng: (10):\(\left( {\frac{2}{5}AA:\frac{3}{5}Aa} \right)\left( {\frac{1}{3}HH:\frac{2}{3}Hh} \right) \times \left( {\frac{1}{3}AA:\frac{2}{3}Aa} \right)\left( {\frac{6}{{11}}Hh:\frac{5}{{11}}hh} \right)\)
Giao tử: \(\left( {\frac{7}{{10}}A:\frac{3}{{10}}a} \right)\left( {\frac{2}{3}H:\frac{1}{3}h} \right) \times \left( {\frac{2}{3}A:\frac{1}{3}a} \right)\left( {\frac{3}{{11}}H:\frac{8}{{11}}h} \right)\)
→ con gái:\(\frac{1}{2}AA\left( {Hh + hh} \right) = \frac{1}{2} \times \frac{7}{{10}} \times \frac{2}{3} \times \left( {1 - \frac{2}{3} \times \frac{3}{{11}}} \right) = \frac{{21}}{{110}}\)
Chọn D



