Vật nhỏ có khối lượng 200g trong một con lắc lò xo dao động điều hòa với chu kì T và biên độ 4cm. Bi

Câu hỏi
Nhận biếtVật nhỏ có khối lượng 200g trong một con lắc lò xo dao động điều hòa với chu kì T và biên độ 4cm. Biết trong một chu kì, khoảng thời gian để vật nhỏ có độ lớn gia tốc không nhỏ hơn \(500\sqrt 2 cm/{s^2}\) là \(\frac{T}{2}\). Độ cứng của lò xo là:
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Độ lớn của gia tốc không nhỏ hơn \(500\sqrt 2 cm/{s^2}\) tức là:
\(\left\{ \begin{gathered}
a \geqslant 500\sqrt 2 (cm/{s^2}) \hfill \\
a \leqslant - 500\sqrt 2 (cm/{s^2}) \hfill \\
\end{gathered} \right.\)
Thời gian để độ lớn của gia tốc không nhỏ hơn \(500\sqrt 2 cm/{s^2}\) là \(\frac{T}{2}\) ứng với góc 1800.
Ta có giản đồ vecto như sau:
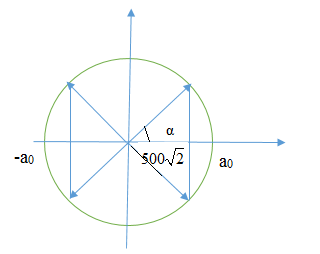
Góc: \(\alpha = \frac{{{{180}^0}}}{4} = {45^0}\)
Ta có: \(500\sqrt 2 = {a_0}.\cos \alpha = {a_0}.\cos {45^0}\)
\( \Rightarrow {a_0} = \frac{{500\sqrt 2 }}{{\cos {{45}^0}}} = {1000_{}}cm/{s^2}\)
Áp dụng công thức:
\({a_0} = {\omega ^2}.A \Rightarrow {\omega ^2} = \frac{{{a_0}}}{A} = \frac{{1000}}{4} = 250\)
\( \Leftrightarrow \frac{k}{m} = 250 \Rightarrow k = 250.0,2 = 50N/m\)
Chọn A.










