Vật dao động điều hòa với phương trình x = Acos ( 8pi t + pi 6 ). Sau một phần tư chu kỳ kể từ thời

Câu hỏi
Nhận biếtVật dao động điều hòa với phương trình \(x = A\cos \left( {8\pi t + \frac{\pi }{6}} \right)\). Sau một phần tư chu kỳ kể từ thời điểm ban đầu vật đi được quãng đường là bao nhiêu
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Pha ban đầu của dao động: \(\varphi = \frac{\pi }{6}\)
Sau thời gian \(\frac{T}{4}\), vật quay được góc: \(\Delta \varphi = \omega .\Delta t = \frac{{2\pi }}{T}.\frac{T}{4} = \frac{\pi }{2}\,\,\left( {rad} \right)\)
Biểu diễn trên VTLG ta có:
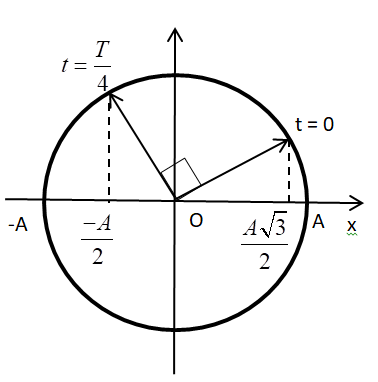
Từ VTLG, ta thấy quãng đường vật đi được là: \(S = \frac{{A\sqrt 3 }}{2} + \frac{A}{2}\)
Chọn A.










