Vật dao động điều hòa với phương trình x = 5cos ( 6pi t + pi 6 ),,cm.

Câu hỏi
Nhận biếtVật dao động điều hòa với phương trình \(x = 5 \cos \left( {6 \pi t + \frac{ \pi }{6}} \right) \, \,cm \). Số lần vật đi qua vị trí x = 2,5 cm theo chiều âm kể từ thời điểm \({t_1} = 2 \, \,s \) đến \({t_2} = 3,25 \, \,s \) là
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Pha ban đầu của dao động: \(\varphi = \frac{\pi }{6}\,\,\left( {rad} \right)\)
Tại thời điểm \({t_1} = 2\,\,s\), vật quay được góc: \(\Delta {\varphi _1} = \omega .{t_1} = 6\pi .2 = 12\pi \,\,\left( {rad} \right)\)
Vật dao động được 6 chu kì và trở về vị trí đầu.
Trong khoảng thời gian từ \({t_1} = 2\,\,s\) đến \({t_2} = 3,25\,\,s\), vật quay được góc:
\(\Delta \varphi = \omega .\Delta t = 6\pi .\left( {3,25 - 2} \right) = 7,5\pi = 6\pi + \frac{{3\pi }}{2}\,\,\left( {rad} \right)\)
Biểu diễn trên vòng tròn lượng giác ta có:
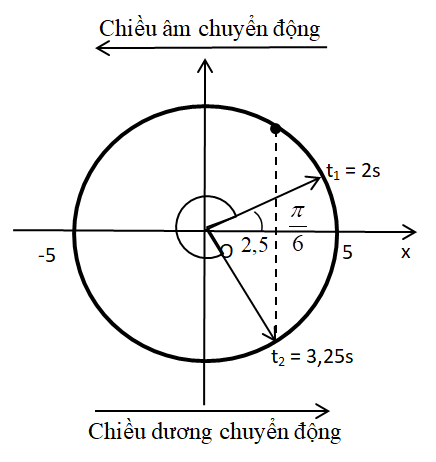
Nhận xét: Trong 1 chu kì, vật đi qua vị trí x = 2,5 cm theo chiều âm 1 lần.
Vậy trong khoảng thời gian từ \({t_1} = 2\,\,s\) đến \({t_2} = 3,25\,\,s\), vật qua vị trí x = 2,5 cm theo chiều âm 4 lần.
Chọn C.










