Vật dao động điều hòa theo phương trình x = Acos ( pi t - pi 6 )cm. Thời điểm vật đi qua vị trí cân

Câu hỏi
Nhận biếtVật dao động điều hòa theo phương trình \(x = A\cos \left( {\pi t - \frac{\pi }{6}} \right)\,\,cm\). Thời điểm vật đi qua vị trí cân bằng là:
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Nhận xét: Trong 1 chu kì, vật đi qua VTCB 2 lần, góc quét giữa hai lần liên tiếp là \(\pi \).
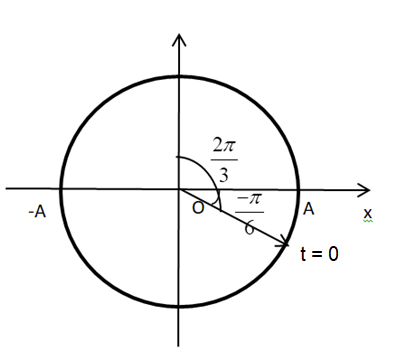
Từ VTLG, ta thấy thời điểm đầu tiên vật đi qua VTCB, góc quét được là \(\frac{{2\pi }}{3}\) → pha của vật tại VTCB: \(\varphi = \frac{{2\pi }}{3} + k\pi \,\,\left( {k \in N} \right)\)
Áp dụng mối liên hệ giữa góc \(\varphi \) và thời điểm t, ta có thời điểm vật đi qua VTCB:
\(t = \frac{\varphi }{\omega } = \frac{{\frac{{2\pi }}{3} + k\pi }}{\pi } = \frac{2}{3} + k\,\,\left( s \right)\,\,\left( {k \in N} \right)\)
Chọn C.










