Vật dao động điều hòa gọi t1 là thời gian ngắn nhất vật đi li độ x = A

Câu hỏi
Nhận biếtVật dao động điều hòa gọi t1 là thời gian ngắn nhất vật đi li độ x = A/2 đến li độ \(x = {{A \sqrt 3 } \over 2} \) và t2 là thời gian ngắn nhất vật đi từ VTCB đến li độ \(x = - {{A \sqrt 2 } \over 2} \) . Mối quan hệ giữa t1 và t2 là
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Biểu diễn các thời điểm trên đường tròn lượng giác ta có:
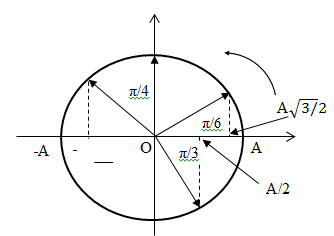
+ Khoảng thời gian ngắn nhất vật đi từ li độ x = A/2đến li độ \(x = {{A\sqrt 3 } \over 2}\) tương ứng với góc quét:
α1 = π/3 + π/6 = π/2 (rad)
\( \Rightarrow {t_1} = {{{\alpha _1}} \over \omega } = {\alpha _1}.{T \over {2\pi }} = {\pi \over 2}{T \over {2\pi }} = {T \over 4}\)
+ Khoảng thời gian ngắn nhất vật đi từ VTCBđến li độ \(x = - {{A\sqrt 2 } \over 2}\) tương ứng với góc quét:
α2 = π/4 (rad)
\( \Rightarrow {t_2} = {{{\alpha _2}} \over \omega } = {\alpha _2}.{T \over {2\pi }} = {\pi \over 4}{T \over {2\pi }} = {T \over 8}\)
=> 2t2 = t1










