Thí nghiệm hiện tượng sóng dừng trên sợi dây đàn hồi có chiều dài L có một đầu cố định một đầu tự do
Câu hỏi
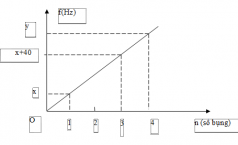
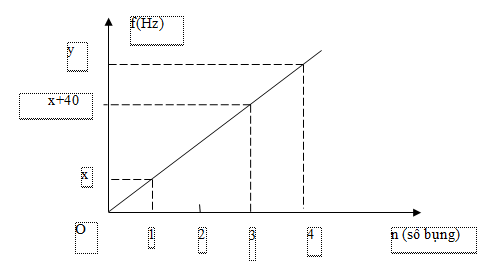
Nhận biếtThí nghiệm hiện tượng sóng dừng trên sợi dây đàn hồi có chiều dài L có một đầu cố định, một đầu tự do. Kích thích sợi dây dao động với tần số f thì khi sảy ra hiện tượng sóng dừng trên sợi dây hình thành các bó sóng. Đồ thị biểu diễn mối quan hệ giữa tần số f và số bụng sóng trên dây như hình bên. Trung bình cộng của x và y là
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Điều kiện để có sóng dừng trên dây một đầu cố định, một đầu tự do là :
L=(2k+1)λ4=(2k+1)v4f
Số bụng sóng là : n = k+1.
Khi n = 1 thì k = 0 nên : L=1.v4x
Khi n = 3 thì k = 2 nên : L=(2.2+1)v4(x+40)
=> v4x=5v4.(x+40)=>x=10Hz
Khi n = 4 thì k = 3 nên:
L=(2.3+1).v4y
Suy ra:
v4x=7v4y=>y=7x=70Hz
Vậy trung bình cộng của x và y là : (x+y)/2 = (10+70)/2=40Hz.











