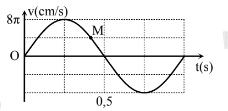
Một vật nhỏ dao động điều hòa trên trục Ox có đồ thị vận tốc của vật phụ thuộc vào thời gian như hìn

Câu hỏi
Nhận biếtMột vật nhỏ dao động điều hòa trên trục Ox có đồ thị vận tốc của vật phụ thuộc vào thời gian như hình bên. Ứng với điểm M trên đồ thị, li độ của vật có giá trị bằng
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Từ đồ thị ta có:
\({v_{max}} = 8\pi \left( {cm/s} \right) = A\omega \)
\({v_M} = 4\pi \left( {cm/s} \right)\)
\(\dfrac{T}{2} = 0,5s \Rightarrow T = 1s\)
\( \Rightarrow \omega = \dfrac{{2\pi }}{T} = 2\pi \left( {rad/s} \right)\)
\( \Rightarrow A = \dfrac{{{v_{max}}}}{\omega } = \dfrac{{8\pi }}{{2\pi }} = 4cm\)
Ta có: \({A^2} = x_M^2 + \dfrac{{v_M^2}}{{{\omega ^2}}}\)
\(\begin{array}{l} \Leftrightarrow {4^2} = x_M^2 + \dfrac{{{{\left( {4\pi } \right)}^2}}}{{{{\left( {2\pi } \right)}^2}}}\\ \Rightarrow \left| {{x_M}} \right| = 2\sqrt 3 cm\end{array}\)
Từ đồ thị thấy, tại điểm M vật đang đi ra xa vị trí cân bằng
\( \Rightarrow {x_M} = 2\sqrt 3 cm\)
Chọn B