Một vật dao động điều hòa với phương trình x = Acos( 2pi t T + pi 2 ). Thời gian ngắn nhất kể từ

Câu hỏi
Nhận biếtMột vật dao động điều hòa với phương trình \(x = Acos\left( {{{2\pi t} \over T} + {\pi \over 2}} \right)\). Thời gian ngắn nhất kể từ lúc bắt đầu dao động tới khi vật có gia tốc bằng một nửa giá trị cực đại là
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Thời điểm ban đầu t = 0 vật qua VTCB theo chiều âm
Vật có gia tốc bằng 1 nửa giá trị cực đại \( \Leftrightarrow - {\omega ^2}x = {{{\omega ^2}A} \over 2} \Rightarrow x = - {A \over 2}\)
Biểu diễn các thời điểm trên đường tròn lượng giác:
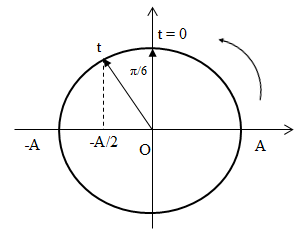
=> Góc quét: α = π/6 (rad) \( \Rightarrow t = {\alpha \over \omega } = {{{\pi \over 6}} \over {{{2\pi } \over T}}} = {T \over {12}}\)










