Một vật dao động điều hòa với phương trình x = 4cos ( 3pi t + pi over

Câu hỏi
Nhận biếtMột vật dao động điều hòa với phương trình \(x = 4 \cos \left( {3 \pi t + { \pi \over 6}} \right)cm \) . Kể từ t = 0, lần thứ 203 vật cách vị trí cân bằng một đoạn 2 cm là?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Chu kì: T = 2π/ω = 2/3 s
+ Vật cách vị trí cân bằng một đoạn 2cm => x = ± 2cm
+ Trong 1 chu kì vật qua vị trí x = ± 2cm 4 lần. Sau 50 chu kì vật qua vị trí x = ± 2cm 200 lần
=> Lần thứ 203 vật qua vị trí x = ± 2cm vào thời điểm: t = 50T + ∆t
+ Biểu diễn trên đường tròn lượng giác :
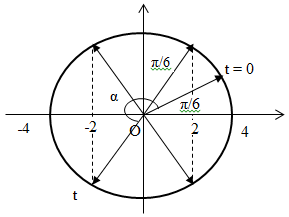
Góc quét được : α = π/3 + π/2 + π/3 = 7π/6 (rad)
\( \Rightarrow \Delta t = {\alpha \over \omega } = {{{{7\pi } \over 6}} \over {3\pi }} = {7 \over {18}}s\)
\( \Rightarrow t = 200T + \Delta t = 200.{2 \over 3} + {7 \over {18}} = {{2407} \over {18}}s\)










