Một vật dao động điều hoà với phương trình x = 10cos(πt + π/3) cm. Khoảng thời gian tính từ lúc vật

Câu hỏi
Nhận biếtMột vật dao động điều hoà với phương trình x = 10cos(πt + π/3) cm. Khoảng thời gian tính từ lúc vật bắt đầu dao động (t = 0) đến khi vật đi được quãng đường 50 cm là
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
+ Chu kì dao động: T = 2s. Biên độ dao động: A = 10cm
+ Vật đi được quãng đường S = 50cm = 40cm + 10cm trong khoảng thời gian: ∆t = 1T + ∆t’.
Trong 1T vật đi được quãng đường 40cm. Vật đi được quãng đường 10cm còn lại trong khoảng thời gian ∆t’ (tương ứng với chất điểm đi từ vị trí (1) đến vị trí (2) trên đường tròn lượng giác).
+ Biểu diễn trên đường tròn lượng giác ta có:
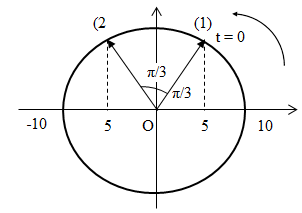
Góc quét được: \(\alpha = {\pi \over 3} \Rightarrow \Delta t' = {\alpha \over \omega } = \alpha .{T \over {2\pi }} = {\pi \over 3}.{T \over {2\pi }} = {T \over 6} = {1 \over 3}s\)
=> Khoảng thời gian vật đi được quãng đường 50cm là: ∆t = T + ∆t’ = 2 + 1/3 = 7/3 (s)










