Một vật dao động điều hòa quanh vị trí cân bằng O. Tại thời điểm t1 vật đi qua vị trí cân bằng. Tron

Câu hỏi
Nhận biếtMột vật dao động điều hòa quanh vị trí cân bằng O. Tại thời điểm t1, vật đi qua vị trí cân bằng. Trong khoảng thời gian từ thời điểm t1 đến thời điểm \({t_2} = {t_1} + \dfrac{1}{6}\,\left( s \right)\)vật không đổi chiều chuyển động và tốc độ của vật giảm còn một nửa. Trong khoảng thời gian từ thời điểm t2 đến thời điểm \({t_3} = {t_2} + \dfrac{1}{6}\,\left( s \right)\), vật đi được quãng đường 6 cm. Tốc độ cực đại của vật trong quá trình dao động là :
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Thời điểm t1 vật qua vị trí cân bằng tốc độ của vật cực đại: \(x = 0;{v_{\max }} = \omega A\)
Thời điểm t2 tốc độ của vật giảm 1 nửa : \(v = \omega \sqrt {{A^2} - {x^2}} = \dfrac{{\omega A}}{2} \Rightarrow x = \pm \dfrac{{\sqrt 3 }}{2}A\)
Thời gian vật đi từ t1 đến t2 là : \(\dfrac{T}{6} = \dfrac{1}{6}s \Rightarrow T = 1s \Rightarrow \omega = \dfrac{{2\pi }}{T} = 2\pi \,\,\left( {rad/s} \right)\)
Thời gian vật đi từ t2 đến t3 là : \(\dfrac{1}{6}s = \dfrac{T}{6}\) nên tại t3 là vị trí \(x = \pm \dfrac{{A\sqrt 3 }}{2}\)
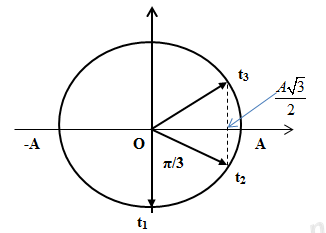
Từ VTLG ta xác định được quãng đường đi được:
\(A - \dfrac{{A\sqrt 3 }}{2} = 3cm \Rightarrow A = 12 + 6\sqrt 3 \,\,\left( {cm} \right)\)
Tốc độ cực đại:
\({v_{m{\rm{ax}}}} = \left( {12 + 6\sqrt 3 } \right)2\pi = 140,695cm/s \approx 1,41m/s\)
Chọn B.










