Một vật có khối lượng 200 g dao động điều hòa quanh vị trí cân bằng. Đồ thị hình bên mô tả động năng

Câu hỏi
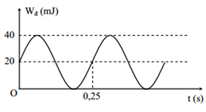
Nhận biếtMột vật có khối lượng 200 g, dao động điều hòa quanh vị trí cân bằng. Đồ thị hình bên mô tả động năng của vật (Wđ) thay đổi phụ thuộc vào thời gian t. Tại t = 0, vật đang có li độ âm. Lấy π2 = 10. Phương trình dao động của vật là
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Từ đồ thị ta thấy động năng biến thiên tuần hoàn chu kỳ 0,25 (s)
Vật dao động điều hòa chu kỳ T = 2.0,25 = 0,5 (s)
Tần số góc của dao động: \(\omega = \dfrac{{2\pi }}{T} = 4\pi \,\,\left( {rad/s} \right)\)
Cơ năng của vật là:
\(\begin{array}{l}W = {W_{d\max }} = \dfrac{1}{2}m{\omega ^2}{A^2} \Rightarrow {40.10^{ - 3}} = \dfrac{1}{2}.0,2.{\left( {4\pi } \right)^2}{A^2}\\ \Rightarrow A = 0,05\,\,\left( m \right) = 5\,\,\left( {cm} \right)\end{array}\)
Tại thời điểm t = 0, động năng của vật là:
\({W_d} = \dfrac{1}{2}m{v^2} \Rightarrow {20.10^{ - 2}} = \dfrac{1}{2}.0,2.{v^2} \Rightarrow {v^2} = 0,2\)
Ta có công thức độc lập với thời gian:
\(\begin{array}{l}{x^2} + \dfrac{{{v^2}}}{{{\omega ^2}}} = {A^2} \Rightarrow {x^2} + \dfrac{{0,2}}{{{{\left( {4\pi } \right)}^2}}} = 0,{05^2}\\ \Rightarrow x = - \dfrac{{0,05\sqrt 2 }}{2}\,\,\left( m \right) = - \dfrac{{5\sqrt 2 }}{2}\,\,\left( {cm} \right)\\ \Rightarrow 5\cos \varphi = - \dfrac{{5\sqrt 2 }}{2} \Rightarrow \cos \varphi = - \dfrac{{\sqrt 2 }}{2} \Rightarrow \varphi = \pm \dfrac{{3\pi }}{4}\,\,\left( {rad} \right)\end{array}\)
Vậy phương trình dao động của vật là: \(x = 5\cos \left( {4\pi t - \dfrac{{3\pi }}{4}} \right)\,\,\left( {cm} \right)\)
Chọn A.










