Một vật chuyển động thẳng có phương trình x=30+4t-t^2(m;s). Tính quãng đường vật đi từ thời điểm t1

Câu hỏi
Nhận biếtMột vật chuyển động thẳng có phương trình \(x=30+4t-{{t}^{2}}(m;s)\). Tính quãng đường vật đi từ thời điểm t1 = 1s đến thời điểm t2 = 3s?
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Từ phương trình tọa độ - thời gian ta thu được phương trình vận tốc \(v=4-2t\to v=0\leftrightarrow t=2\text{s}\) , vật sẽ đổi chiều chuyển động sau 2 s.
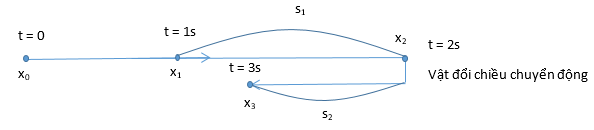
Do vậy quãng đường đi được của vật được tính: \(s={{s}_{1}}+{{s}_{2}}=\left| {{x}_{2}}-{{x}_{1}} \right|+\left| {{x}_{3}}-{{x}_{2}} \right|=\left| 4-3 \right|+\left| 3-4 \right|=2m\)
Chọn A










