Một con lắc lò xo treo thẳng đứng tại vị trí cân bằng lò xo dãn Delta l kích thích cho con lắc dao đ

Câu hỏi
Nhận biếtMột con lắc lò xo treo thẳng đứng, tại vị trí cân bằng lò xo dãn \(\Delta l\), kích thích cho con lắc dao động điều hòa theo phương thẳng đứng với chu kì T. Trong một chu kỳ khoảng thời gian để lực đàn hồi tác dụng vào vật cùng chiều với trọng lực là \(\dfrac{T}{4}\). Biên độ dao động của vật là :
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
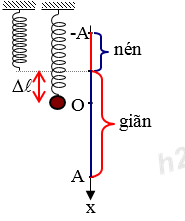
Ta có trọng lực tác dụng vào vật luôn có phương thẳng đứng, chiều hướng từ trên xuống.
Lực đàn hồi tác dụng vào vật có xu hướng đưa lò xo về trạng thái không biến dạng, do đó lực đàn hồi có chiều hướng từ trên xuống khi lò xo bị nén.
Biểu diễn trên hình vẽ ta có:
Biểu diễn trên VTLG ta có:
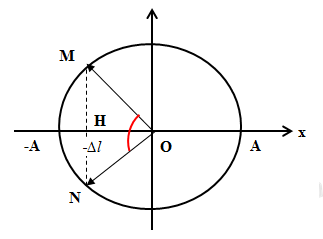
Trong một chu kỳ khoảng thời gian để lực đàn hồi tác dụng vào vật cùng chiều với trọng lực (vật quay từ M đến N) là \(\dfrac{T}{4}\) tương ứng với góc quét : \(\alpha = \omega .\Delta t = \dfrac{{2\pi }}{T}.\dfrac{T}{4} = \dfrac{\pi }{2}\)
Suy ra \(\widehat {MOH} = \dfrac{\pi }{4}\)
Xét ∆MOH có : \(\cos \widehat {MOH} = \dfrac{{OH}}{{OM}} \Leftrightarrow \cos \dfrac{\pi }{4} = \dfrac{{\Delta l}}{A} \Rightarrow A = \sqrt 2 .\Delta l\)
Chọn C.










