Một con lắc lò xo gồm một vật nhỏ có khối lượng m = 200 g và lò xo có độ cứng k đang dao động điều h

Câu hỏi
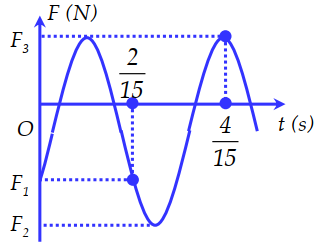
Nhận biếtMột con lắc lò xo gồm một vật nhỏ có khối lượng m = 200 g và lò xo có độ cứng k, đang dao động điều hòa theo phương thẳng đứng. Chọn gốc tọa độ ở vị trí cân bằng, chiều dương hướng xuống dưới. Đồ thị biểu diễn sự phụ thuộc của lực đàn hồi theo thời gian được cho như hình vẽ. Biết \({F_1} + 3{F_2} + 6{F_3} = 0\). Lấy \(g = 10\,\,m/{s^2}\). Tỉ số thời gian lò xo giãn với thời gian lò xo nén trong một chu kì gần giá trị nào nhất sau đây?
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Ở thời điểm ban đầu, lực đàn hồi \({F_1} = k.\left( {\Delta l + x} \right)\)
Khi vật đi qua vị trí biên dương, lực đàn hồi \({F_2} = - k.\left( {\Delta l + A} \right)\)
Khi vật đi qua vị trí biên âm, lực đàn hồi \({F_3} = - k.\left( {\Delta l - A} \right)\)
Từ trục thời gian trên đồ thị, ta thấy chu kì của con lắc:
\(T = \frac{4}{{15}} - \left( {\frac{2}{{15}}:2} \right) = \frac{1}{5}\,\,\left( s \right) = 0,2\,\,\left( s \right)\)
Ta có VTLG:
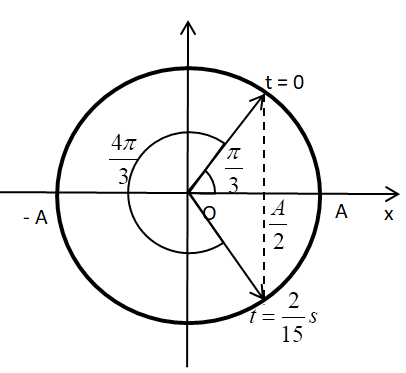
Từ VTLG, ta thấy từ thời điểm t = 0 đến thời điểm \(t = \frac{2}{{15}}s\), vật quay được góc:
\(\Delta \varphi = \omega .\Delta t = \frac{{2\pi }}{T}.\Delta t = \frac{{2\pi }}{{0,2}}.\frac{2}{{15}} = \frac{{4\pi }}{3}\,\,\left( {rad} \right)\)
Tại thời điểm t = 0, li độ của vật: \(x = A.cos\frac{\pi }{3} = \frac{A}{2}\)
\( \Rightarrow {F_1} = - k.\left( {\Delta l + x} \right) = - k.\left( {\Delta l + \frac{A}{2}} \right)\)
Theo đề bài ta có: \({F_1} + 3{F_2} + 6{F_3} = 0\)
\(\begin{gathered}\Rightarrow - k.\left( {\Delta l + \frac{A}{2}} \right) + 3.\left( { - k} \right).\left( {\Delta l + A} \right) + 6.\left( { - k} \right).\left( {\Delta l - A} \right) = 0 \hfill \\\Rightarrow \left( {\Delta l + \frac{A}{2}} \right) + 3.\left( {\Delta l + A} \right) + 6.\left( {\Delta l - A} \right) = 0 \hfill \\\Rightarrow \Delta l = \frac{A}{4} \hfill \\ \end{gathered} \)
Thời gian lò xo nén trong 1 chu kỳ:
\({t_{nen}} = 2.\frac{{{\text{ar}}\cos \left( { - \frac{{\Delta l}}{A}} \right)}}{\omega } = 2.\frac{{{\text{ar}}\cos \left( { - \frac{{\Delta l}}{A}} \right)}}{{\frac{{2\pi }}{T}}} = \frac{{T.{\text{ar}}\cos \left( {\frac{{\Delta l}}{A}} \right)}}{\pi } = \frac{{0,2.{\text{ar}}\cos \left( {\frac{1}{4}} \right)}}{\pi } = 0,084\,\,\left( s \right)\)
Tỉ số thời gian lò xo giãn và nén trong 1 chu kì:
\(\frac{{{t_{gian}}}}{{{t_{nen}}}} = \frac{{T - {t_{nen}}}}{{{t_{nen}}}} = \frac{{0,2 - 0,084}}{{0,084}} = 1,38\)
Chọn B.










