Một con lắc đơn dao động với biên độ góc alpha 0 = 5^0. Chu kỳ dao độn

Câu hỏi
Nhận biếtMột con lắc đơn dao động với biên độ góc \({ \alpha _0} = {5^0} \). Chu kỳ dao động là 1s. Tìm thời gian ngắn nhất để vật đi từ vị trí cân bằng về vị trí có li độ góc \( \alpha = 2,{5^0} \)?
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Biểu diễn các vị trí trên VTLG ta được:
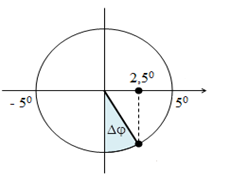
Từ VTLG ta có góc quét được là: \(\Delta \varphi = \dfrac{\pi }{6}\)
Thời gian ngắn nhất để vật đi từ vị trí cân bằng về vị trí có li độ góc \(\alpha = 2,{5^0}\) là:
\(\Delta t = \dfrac{{\Delta \varphi }}{\omega } = \Delta \varphi .\dfrac{T}{{2\pi }} = \dfrac{\pi }{6}.\dfrac{1}{{2\pi }} = \dfrac{1}{{12}}s\)
Chọn C.










