Một chất điểm dao động điều hoà trên trục Ox có vận tốc bằng 0 tại hai thời điểm liên tiếp t1 = 1,75

Câu hỏi
Nhận biếtMột chất điểm dao động điều hoà trên trục Ox có vận tốc bằng 0 tại hai thời điểm liên tiếp \({t_1} = 1,75\,\,s\) và \({t_2} = 2,5\,\,s\), tốc độ trung bình trong khoảng thời gian đó là 16 cm/s. Toạ độ chất điểm tại thời điểm \({t_0} = 0\) là
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Nhận xét: khoảng thời gian giữa hai lần liên tiếp chất điểm có vận tốc bằng không là \(\frac{T}{2}\)
\( \Rightarrow {t_2} - {t_1} = \frac{T}{2} \Rightarrow \frac{T}{2} = 2,5 - 1,75 = 0,75 \Rightarrow T = 1,5\,\,\left( s \right)\)
Trong khoảng thời gian từ \({t_1} = 1,75\,\,s\) và \({t_2} = 2,5\,\,s\), ta có:
Quãng đường vật chuyển động: s = 2.A
Vậy tốc độ trung bình của chất điểm trong khoảng thời gian đó là:
\({v_{tb}} = \frac{s}{{\Delta t}} \Rightarrow \frac{{2A}}{{0,75}} = 16 \Rightarrow A = 6\,\,\left( {cm} \right)\)
Giả sử tại thời điểm \({t_2} = 2,5\,\,s\), chất điểm đang ở biên dương.
Vậy tại thời điểm \({t_2} = 2,5\,\,s\), chất điểm quay được góc:
\(\Delta \varphi = \omega .{t_2} = \frac{{2\pi }}{T}.{t_2} = \frac{{2\pi }}{{1,5}}.2,5 = \frac{{10\pi }}{3} = 2\pi + \frac{{4\pi }}{3}\,\,\left( {rad} \right)\)
Biểu diễn trên VTLG, ta có:
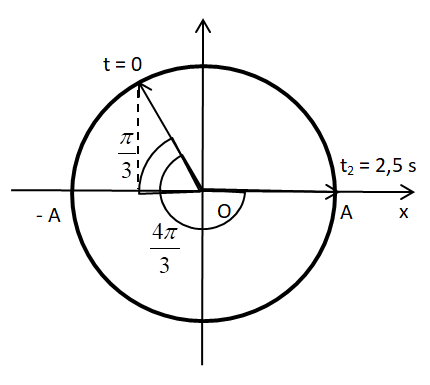
Từ VTLG, ta thấy tọa độ chất điểm tại thời điểm ban đầu:
\(x = - A\cos \frac{\pi }{3} = - 6.cos\frac{\pi }{3} = - 3\,\,\left( {cm} \right)\)
Chọn D.










