Một chất điểm dao động điều hòa có vận tốc cực đại 60 cm/s và gia tốc cực đại là 2π m/s2. Chọn mốc t

Câu hỏi
Nhận biếtMột chất điểm dao động điều hòa có vận tốc cực đại 60 cm/s và gia tốc cực đại là 2π m/s2. Chọn mốc thế năng tại vị trí cân bằng. Thời điểm ban đầu (t = 0), chất điểm có vận tốc 30 cm/s và thế năng đang tăng. Chất điểm có gia tốc bằng π m/s2 lần đầu tiên ở thời điểm
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Ta có vận tốc cực đại và gia tốc cực đại của vật:
\(\left\{ \begin{array}{l}{v_{\max }} = \omega A = 60\\{a_{\max }} = {\omega ^2}A = 200\pi \end{array} \right. \Rightarrow \left\{ \begin{array}{l}A = \dfrac{{18}}{\pi }\,\,\left( {cm} \right)\\\omega = \dfrac{{10\pi }}{3}\,\,\left( {rad/s} \right)\end{array} \right.\)
Tại thời điểm ban đầu t = 0, vật có vận tốc v > 0 và thế năng đang tăng, vật chuyển động đến biên, ta có:
\({x_0}^2 + \dfrac{{{v_0}^2}}{{{\omega ^2}}} = {A^2} \Rightarrow {x_0}^2 + \dfrac{{{{30}^2}}}{{{{\left( {\dfrac{{10\pi }}{3}} \right)}^2}}} = {\left( {\dfrac{{18}}{\pi }} \right)^2} \Rightarrow {x_0} = \pm \dfrac{{18\sqrt 3 }}{{2\pi }}\,\,\left( {cm} \right) = \pm A\dfrac{{\sqrt 3 }}{2}\)
Ở thời điểm chất điểm có gia tốc 100π cm/s2 lần đầu tiên, ta có:
\(a = - {\omega ^2}x \Rightarrow 100\pi = - {\left( {\dfrac{{10\pi }}{3}} \right)^2}x \Rightarrow x = - \dfrac{9}{\pi }\,\,\left( {cm} \right) = - \dfrac{A}{2}\)
Ta có vòng tròn lượng giác:
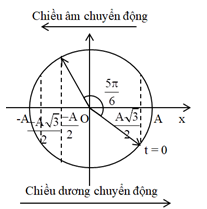
Từ vòng tròn lượng giác, ta thấy tại thời điểm vật có gia tốc 100π cm/s2 lần đầu tiên, vecto quay được góc \(\dfrac{{5\pi }}{6}\,\,rad\)
Thời điểm vật có gia tốc 100π cm/s2 lần đầu tiên là:
\(\Delta t = \dfrac{{\Delta \varphi }}{\omega } = \dfrac{{\dfrac{{5\pi }}{6}}}{{\dfrac{{10\pi }}{3}}} = 0,25\,\,\left( s \right)\)
Chọn C.










