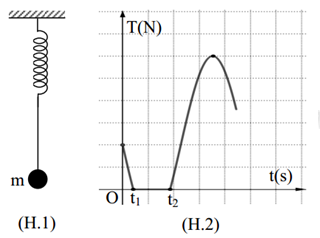
Lò xo nhẹ một đầu cố định đầu còn lại gắn vào sợi dây mềm không dãn có treo vật nhỏ m như hình vẽ (H

Câu hỏi
Nhận biếtLò xo nhẹ một đầu cố định, đầu còn lại gắn vào sợi dây mềm, không dãn có treo vật nhỏ m như hình vẽ (H.1). Khối lượng dây và sức cản của không khí không đáng kể. Tại \(t = 0\), m đang đứng yên ở vị trí cân bằng thì được truyền vận tốc \({v_0}\) thắng đứng từ dưới lên. Sau đó lực căng dây T tác dụng vào m phụ thuộc thời gian theo quy luật được mô tả bởi đồ thị hình vẽ (H.2). Biết lúc vật cân bằng lò xo giãn \(10cm\) và trong quá trình chuyển động m không va chạm với lò xo. Quãng đường m đi được kể từ lúc bắt đầu chuyển động đến thời điểm \({t_2}\) bằng
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Ta có:
\(\Delta {l_0} = 10cm\)
Lực căng dây \(T = {F_{dh}}\)
\( \Rightarrow \) \({T_{max}}\) khi \({F_{d{h_{max}}}}\)
Tại thời điểm ban đầu: \(t = 0\) thì \(T = \dfrac{2}{6}{T_{max}}\) lực đàn hồi khi này \({F_{d{h_0}}} = k.\Delta {l_0} = \dfrac{1}{3}{T_{max}}\)
\(\begin{array}{l} \Rightarrow \dfrac{{{F_{d{h_0}}}}}{{{F_{d{h_{max}}}}}} = \dfrac{{\dfrac{1}{3}{T_{max}}}}{{{T_{max}}}} = \dfrac{1}{3} = \dfrac{{k\Delta {l_0}}}{{k\left( {\Delta {l_0} + A} \right)}}\\ \Rightarrow A = 2\Delta {l_0} = 20cm\end{array}\)
Dây trùng khi lò xo nén và dây căng khi lò xo dãn
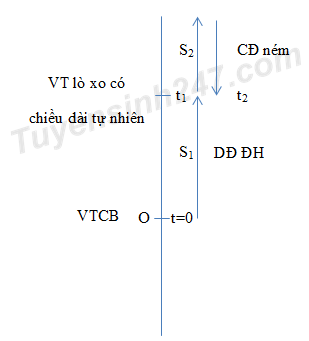
Ta có: \({S_1} = 10cm\)
\({S_2} = {h_{max}}\) ta có \(\dfrac{1}{2}m{v^2} = mg{h_{max}}\)
\( \Rightarrow {S_2} = \dfrac{{{v^2}}}{{2g}}\)
Lại có vị trí ném có li độ \(x = - \Delta {l_0} = - \dfrac{A}{2}\) suy ra vận tốc tại đó: \(v = - \omega A\dfrac{{\sqrt 3 }}{2}\)
\( \Rightarrow {S_2} = \dfrac{{3{A^2}}}{{8\Delta {l_0}}} = \dfrac{{{{3.20}^2}}}{{8.10}} = 15cm\)
\( \Rightarrow \) Quãng đường vật m đi được từ thời điểm ban đầu đến \({t_2}\) là: \(S = {S_1} + 2{S_2} = 10 + 2.15 = 40cm\)
Chọn B