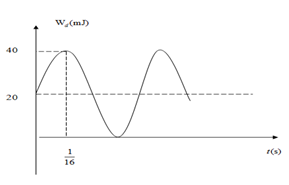
Đồ thị biểu diễn sự biến thiên động năng của một vật dao động điều hòa cho ở hình vẽ bên. Biết vật n

Câu hỏi
Nhận biếtĐồ thị biểu diễn sự biến thiên động năng của một vật dao động điều hòa cho ở hình vẽ bên. Biết vật nặng 200g. Lấy π2 = 10. Phương trình dao động của vật là
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Đáp án C
Tại thời điểm ban đầu thì động năng bằng 1 nửa giá trị động năng cực đại, tức là thế năng bằng 1 nửa thế năng cực đại hay cơ năng.
Ta có: \(\frac{1}{2}.k.{x^2} = \frac{1}{2}.\frac{1}{2}.k.{A^2} \Rightarrow x = \frac{A}{{\sqrt 2 }}\)
Có hình vẽ sau:
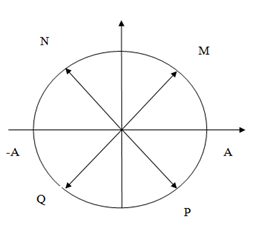
Vì ban đầu động năng đang tăng, tức là thế năng đang giảm, nên vị trí ban đầu là vị trí Q, suy ra pha ban đầu là \(\frac{{ - 3\pi }}{4}\)
Từ đồ thị ta thấy từ thời điểm ban đầu đến khi động năng đạt giá trị cực đại lần đâu tiên thì hết thời gian là 1/16 giây.
Vậy: \(\frac{1}{{16}}s = \frac{1}{4}T' \Rightarrow T' = \frac{4}{{16}}s \Rightarrow \omega ' = \frac{{2\pi }}{{T'}} \Rightarrow \omega = \frac{1}{2}\omega ' = 4\pi rad/s\)
Động năng cực đại bằng 40mJ nên ta có:
\(\frac{1}{2}.m.{\omega ^2}.{A^2} = 40mJ \Leftrightarrow \frac{1}{2}.0,2.{(4\sqrt {10} )^2}.{A^2} = {40.10^{ - 3}} \Rightarrow A = 0,05m = 5cm\)
Vậy phương trình dao động là : \(x = 5\cos \left( {4\pi t - \frac{{3\pi }}{4}} \right)cm\)