Đặt điện áp u = 160căn 2 cos ( 100pi t )( V )vào hai đầu đoạn mạch mắ

Câu hỏi
Nhận biếtĐặt điện áp \(u = 160 \sqrt 2 \cos \left( {100 \pi t} \right) \left( V \right) \)vào hai đầu đoạn mạch mắc nối tiếp gồm điện trở \(R = 40 \sqrt 3 \Omega \)tụ điện và cuộn cảm thuần có độ tự cảm L thay đổi được điều chỉnh độ tự cảm đến giá trị L = Lm để điện áp hiệu dụng hai đầu cuộn cảm đạt giá trị cực đại và bằng 320 V. Biểu thức cường độ dòng điện trong mạch khi đó là
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Cách giải:
Khi L thay đổi để \({U_{{L_{max}}}}\) ta có \(U \bot {U_{RC}}\) biểu diễn trên giản đồ Vecto ta được
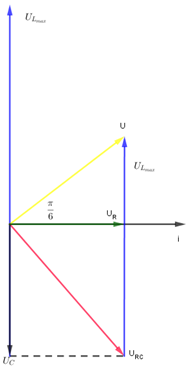
Khi đó ta có \({U^2} + U_{RC}^2 = U_{{L_{max}}}^2 = > {160^2} + U_{RC}^2 = {320^2} = > {U_{RC}} = 160\sqrt 3 V\)
Áp dụng hệ thức lượng trong tam giác vuông ta có \(\frac{1}{{U_R^2}} = \frac{1}{{{U^2}}} + \frac{1}{{U_{RC}^2}} = > \frac{1}{{U_R^2}} = \frac{1}{{{{160}^2}}} + \frac{1}{{{{\left( {160\sqrt 3 } \right)}^2}}} = > {U_R} = 80\sqrt 3 V\)
Cường độ dòng điện hiệu dụng qua mạch là \(I = \frac{{{U_R}}}{R} = \frac{{80\sqrt 3 }}{{40\sqrt 3 }} = 2A\)
Độ lệch pha giữa u và i là \(cos\varphi = \frac{{{U_R}}}{U} = \frac{{80\sqrt 3 }}{{160}} = \frac{{\sqrt 3 }}{2} = > \varphi = \frac{\pi }{6} = > {\varphi _i} = {\varphi _u} - \varphi = 0 - \frac{\pi }{6} = - \frac{\pi }{6}\)
Biểu thức cường độ dòng điện chạy qua mạch là \(i = 2\sqrt 2 \cos \left( {100\pi t - \frac{\pi }{6}} \right)\left( A \right)\)
Chọn C










