Con lắc lò xo dao động theo phương ngang với phương trình x = Acos(omega t + varphi ) . Cứ sau những

Câu hỏi
Nhận biếtCon lắc lò xo dao động theo phương ngang với phương trình \(x = Acos(\omega t + \varphi )\) . Cứ sau những khoảng thời gian bằng nhau và bằng \(\frac{\pi }{{40}}\left( s \right)\) thì động năng của vật bằng thế năng của lò xo. Con lắc dao động điều hoà với tần số góc
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Hướng dẫn giải:
Ta có:
\({{\rm{W}}_t} = {{\rm{W}}_d} \to 2{{\rm{W}}_t} = {\rm{W}} \to x = \pm {A \over {\sqrt 2 }}\)
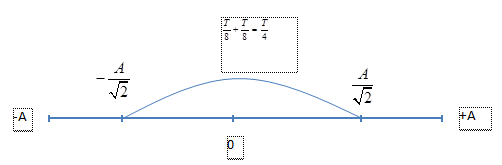
Ta có, khoảng thời gian giữa hai lần liên tiếp động năng bằng thế năng là \(\frac{T}{4}\)
Theo đầu bài, ta có:
\(\begin{array}{l}\frac{\pi }{{40}} = \frac{T}{4} \to T = \frac{\pi }{{10}}\\\omega = \frac{{2\pi }}{T} = \frac{{2\pi }}{{\frac{\pi }{{10}}}} = 20(ra{\rm{d}}/s)\end{array}\)
=> Chọn A










