Ba điểm sáng cùng dao động điều hòa dọc theo trục Ox, xung quanh vị trí cân bằng O, cùng tần số. Đồ

Câu hỏi
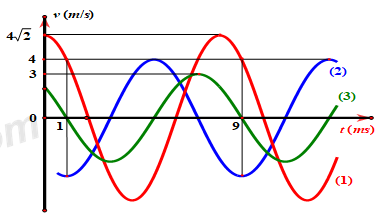
Nhận biếtBa điểm sáng cùng dao động điều hòa dọc theo trục Ox, xung quanh vị trí cân bằng O, cùng tần số. Đồ thị vận tốc v của các điểm sáng phụ thuộc thời gian t như hình bên. Tổng li độ của các chất điểm ở cùng một thời điểm có giá trị lớn nhất bằng:
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Từ đồ thị, ta thấy chu kì của vận tốc là:
\(T = 9 - 1 = 8\,\,\left( {ms} \right) \Rightarrow \omega = \dfrac{{2\pi }}{T} = \dfrac{{2\pi }}{{0,008}} = 250\,\,\left( {rad/s} \right)\)
Xét đồ thị (1) ở thời điểm đầu có vận tốc \({v_{1\max }} = 4\sqrt 2 \,\,\left( {m/s} \right)\), phương trình vận tốc của vật 1 là:
\({v_1} = 4\sqrt 2 \cos \left( {250\pi t} \right)\,\,\left( {m/s} \right) \Rightarrow {x_1} = \dfrac{{4\sqrt 2 }}{{250\pi }}\cos \left( {250\pi t - \dfrac{\pi }{2}} \right)\,\,\left( m \right)\)
Xét đồ thị (2), ở thời điểm t = 1 (ms) có vận tốc \({v_{2\min }} = - 4\,\,\left( {m/s} \right)\), phương trình vận tốc của vật 2 là:
\(\begin{array}{l}{v_2} = 4\cos \left[ {250\pi \left( {t - 0,001} \right) + \pi } \right] = 4\cos \left( {250\pi t + \dfrac{{3\pi }}{4}} \right)\,\,\left( {m/s} \right)\\ \Rightarrow {x_2} = \dfrac{4}{{250\pi }}\cos \left( {250\pi t + \dfrac{\pi }{4}} \right)\,\,\left( m \right)\end{array}\)
Xét đồ thị (3), ở thời điểm t = 1 (ms) có vận tốc \({v_3} = 0\,\,\left( {m/s} \right)\) và đang giảm, phương trình vận tốc của vật 3 là:
\(\begin{array}{l}{v_3} = 3\cos \left[ {250\pi \left( {t - 0,001} \right) + \dfrac{\pi }{2}} \right] = 3\cos \left( {250\pi t + \dfrac{\pi }{4}} \right)\,\,\left( {m/s} \right)\\ \Rightarrow {x_3} = \dfrac{3}{{250\pi }}\cos \left( {250\pi t - \dfrac{\pi }{4}} \right)\end{array}\)
Tổng li độ của 3 dao động là:
\(\begin{array}{l}x = {x_1} + {x_2} + {x_3} = \dfrac{{4\sqrt 2 }}{{250\pi }}\angle - \dfrac{\pi }{2} + \dfrac{4}{{250\pi }}\angle \dfrac{\pi }{4} + \dfrac{3}{{250\pi }}\angle - \dfrac{\pi }{4} = \dfrac{7}{{250\pi }}\angle - \dfrac{\pi }{4}\\ \Rightarrow \left\{ \begin{array}{l}A = \dfrac{7}{{250\pi }}\,\,\left( m \right) = 0,89\,\,\left( {cm} \right)\\\varphi = - \dfrac{\pi }{4}\,\,\left( {rad} \right)\end{array} \right.\end{array}\)
Vậy tổng li độ của 3 dao động có độ lớn cực đại là: \({x_{\max }} = A = 0,89\,\,\left( {cm} \right)\)
Chọn A.










