Đặt vào hai đầu đoạn chứa biến trở R một nguồn điện ξ = 20 V và điện trở trong r. Thay đổi giá trị c
Câu hỏi
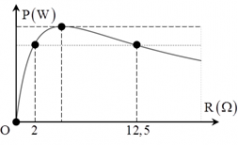
Nhận biếtĐặt vào hai đầu đoạn chứa biến trở R một nguồn điện ξ = 20 V và điện trở trong r. Thay đổi giá trị của biến trở thì thấy đồ thị công suất tiêu thụ trên toàn mạch có dạng như hình vẽ. Công suất tiêu thụ cực đại trên mạch là:
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Đáp án B
Từ đồ thị ta có: $${R_1} = 2\Omega ,{R_2} = 12,5\Omega $$
và $${P_1} = {P_2} \to {{{\zeta ^2}{R_1}} \over {{{\left( {{R_1} + r} \right)}^2}}} = {{{\zeta ^2}{R_2}} \over {{{\left( {{R_2} + r} \right)}^2}}} \to ({R_2} + r) = 2,5({R_1} + r) \to r = 5\Omega $$
Ta có Công suất tiêu thụ trên mạch : $$P = {{{\zeta ^2}R} \over {{{(R + r)}^2}}} = {{{\zeta ^2}} \over {{{(\sqrt R + {r \over {\sqrt R }})}^2}}}$$
P lớn nhất khi $\sqrt R + {r \over {\sqrt R }}$ nhỏ nhất, suy ra: R = r = 5 thì $${P_{\max }} = {{{\zeta ^2}R} \over {{{(R + r)}^2}}} = {{{{20}^2}.5} \over {{{(2.5)}^2}}} = 20W$$










