Một sóng điện từ lan truyền trong chân không dọc theo đường thẳng từ điểm M đến điểm N cách nhau 45

Câu hỏi
Nhận biếtMột sóng điện từ lan truyền trong chân không dọc theo đường thẳng từ điểm M đến điểm N cách nhau 45 m. Biết sóng này có thành phần điện trường tại mỗi điểm biến thiên điều hòa theo thời gian với tần số 5 MHz. Lấy c = 3.108 m/s. Ở thời điểm t, cường độ điện trường tại M bằng 0. Thời điểm nào sau đây cường độ điện trường tại N bằng 0?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Ta có:
+ Chu kì dao động của sóng: \(T=\frac{1}{f}=\frac{1}{{{5.10}^{6}}}={{2.10}^{7}}s\)
+ Độ lệch pha giữa M và N là: \(\Delta \varphi =\frac{2\pi d}{\lambda }=\frac{2\pi .d}{cT}=\frac{2\pi .45}{{{3.10}^{8}}{{.2.10}^{-7}}}=\frac{3\pi }{2}\)
Vẽ trên vòng tròn lượng giác ta được:
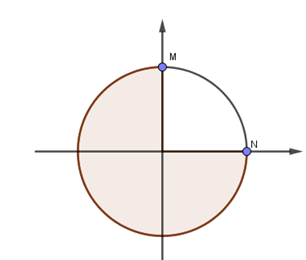
=> thời gian ngắn nhất để cường độ điện trường tại N bằng 0 là: \(\frac{T}{4}=\frac{{{2.10}^{-7}}}{4}={{50.10}^{-9}}=50ns\)
=> Thời điểm mà cường độ điện trường tại N bằng 0 là: \(t'=t+\left( 2n+1 \right)\frac{T}{4}\) với n là số nguyên
Thay vào các phương án ta suy ra đáp án D










