Một con lắc lò xo treo thẳng đứng lò xo có độ cứng 100 N/m, vật dao độ

Câu hỏi
Nhận biếtMột con lắc lò xo treo thẳng đứng lò xo có độ cứng 100 N/m, vật dao động có khối lượng 100g, lấy gia tốc trọng trường g = π2 = 10m/s2. Từ vị trí cân bằng kéo vật xuống một đoạn 1cm rồi truyền cho vật vận tốc đầu \(10 \sqrt 3 \pi cm/s \) hướng thẳng đứng thì vật dao động điều hòa. Thời gian lò xo bị nén trong một chu kỳ là:
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Hướng dẫn giải:
Ta có:
+ Tần số góc của dao động: \(\omega = \sqrt {\frac{k}{m}} = \sqrt {\frac{{100}}{{0,1}}} = 10\pi (ra{\rm{d}}/s)\)
+ Biên độ dao động: \({A^2} = {x^2} + \frac{{{v^2}}}{{{\omega ^2}}} = {1^2} + {\left( {\frac{{10\pi \sqrt 3 }}{{10\pi }}} \right)^2} \to A = 2cm\)
Độ dãn của lò xo tại VTCB: \(\Delta l = \frac{{mg}}{k} = \frac{{0,1.10}}{{100}} = 0,01 = 1cm\)
Chọn chiều dương hướng xuống, ta có:
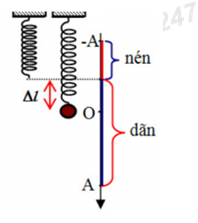
=> Thời gian lò xo bị nén trong 1 chu kì là: \(t = 2\frac{T}{6} = \frac{T}{3} = \frac{{\frac{{2\pi }}{\omega }}}{3} = \frac{1}{{15}}s\)
=> Chọn B










