Cho cơ hệ như hình vẽ, vật m1, m2 nối với nhau nhờ sợi dây nhẹ, không
Câu hỏi
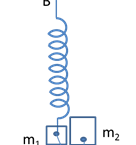
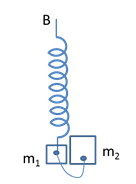
Nhận biếtCho cơ hệ như hình vẽ, vật m1, m2 nối với nhau nhờ sợi dây nhẹ, không dãn có chiều dài l, ban đầu lò xo không biến dạng, đầu B của lò xo để tự do. Biết k=100N/m, m1=400g, m2=600g, lấy g=10=π2(m/s2). Bỏ qua mọi ma sát. Ban đầu (t=0) giữ cho vật m1 và m2 nằm trên mặt phẳng nằm ngang và sau đó thả cho hệ rơi tự do, khi hệ vật rơi đạt được tốc độ $${v_0} = 20\pi (cm/s)$$ thì giữ cố định điểm B và ngay sau đó vật m1 đi thêm được 1 đoạn 4cm thì sợi dây nối giữa hai vật căng. Thời điểm đầu tiên chiều dài của lò xo cực đại là:
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Đáp án D
Khoảng thời gian rơi tự do của hệ là : $$\Delta {t_1} = {{{v_0}} \over g} = {{0,2\pi } \over {10}} = 0,02\pi {\rm{ }}m/s$$
Ta có:
$$\eqalign{ & \Delta {l_{01}} = {{{m_1}g} \over k}{\rm{ = 4cm va }}\Delta {l_{02}} = {{{m_2}g} \over k} = 6cm \cr & {\omega _1} = \sqrt {{k \over {{m_1}}}} = 5\pi (ra{\rm{d}}/s),\omega = \sqrt {{k \over {{m_1} + {m_2}}}} = 10(ra{\rm{d}}/s) \cr} $$
Sau khi giữ cố định B, thì ngay sau đó m1 dao động điều hòa còn m2 tiếp tục rơi tự do
m1 dao động điều hòa quanh vị trí cân bằng O1(Chọn chiều dương thẳng đứng xuống dưới) với li độ x=-4cm và vận tốc $${v_0} = 20\pi (cm/s)$$ => Biên độ dao động của m1 là:
$${A_1} = \sqrt {{x_1}^2 + {{{{{v_1}} \over {{\omega ^2}}}}^2}} = 4\sqrt 2 cm$$
Khi m1 đi xuống thêm được quãng đường $$\Delta {l_{01}} = 4cm$$ thì sợi dây bắt đầu căng, lúc này vận tốc của m1và m2 là: $${v_1} = {v_{1m{\rm{ax}}}} = {A_1}{\omega _1} = 20\pi \sqrt 2 cm/s,{v_2} = {v_0} + g\Delta {t_2}$$
với $$\Delta {t_2}$$ là khoảng thời gian m1 bắt đầu dao động điều hòa đến khi sợi dây bắt đầu căng, khoảng thời gian này ứng với m1 dao động từ li độ -4cm đến 0cm $$ \to \Delta {t_2} = {{{T_1}} \over 8} = 0,05{\rm{s}} \to {v_2} = 1,1283m/s$$
Khi sợi dây bắt đầu căng thì hệ m1+m2 bắt đầu dao động điều hòa quanh VTCB O với vận tốc và vị trí ban đầu là:
$$\left\{ \matrix{ x = - 6cm \hfill \cr v = {{{m_1}{v_1} + {m_2}{v_2}} \over {{m_1} + {m_2}}} = 1,0324m/s = 103,24cm/s \hfill \cr} \right.$$
=> Biên độ dao động của hệ: $$A = \sqrt {{x^2} + {{{v \over {{\omega ^2}}}}^2}} = 11,94cm$$
Hệ m1+m2 xuống thấp nhất thì chiều dài lò xo cực đại, lúc này x= A.
Khoảng thời gian kể từ khi m1+m2 bắt đầu dao động điều hòa đến khi x=A là ∆t, khoảng thời gian này hệ vật đi từ li độ x=-6cm theo chiều dương đến khi x=11,9cm lần đầu.
Dựa vào đường tròn lượng giác:
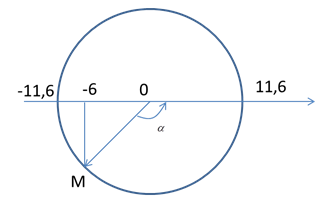
Ta xác định được: $$\alpha = 2,0973{\rm{r}}a{\rm{d}} \to \Delta t = {\alpha \over \omega } = 0,20973{\rm{s}}$$
Vậy thời điểm đầu tiên chiều dài lò xo đạt cực đại là: $$t = \Delta {t_1} + \Delta {t_2} + \Delta t = 0,02\pi + 0,05 + 0,20973 = 0,323{\rm{s}}$$










