Một sóng cơ học lan truyền trên mặt thoáng chất lỏng nằm ngang với tần

Câu hỏi
Nhận biếtMột sóng cơ học lan truyền trên mặt thoáng chất lỏng nằm ngang với tần số 10Hz, tốc đô ̣ truyền sóng 1,2m/s. Hai điểm M và N thuộc măṭ thoáng, trên cùng một phương truyền sóng, cách nhau 26cm (M nằm gần nguồn sóng hơn). Tại thời điểm t, điểm N ha ̣xuống thấp nhất. Khoảng thời gian ngắn nhất sau đó điểm M ha ̣xuống thấp nhất là
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Bước sóng: \(\lambda = \dfrac{v}{f} = \dfrac{{1,2}}{{10}} = 0,12m = 12cm\)
Độ lệch pha giữa hai điểm M và N là: \(\Delta \varphi = \dfrac{{2\pi .d}}{\lambda } = \dfrac{{2\pi .26}}{{12}} = \dfrac{{13\pi }}{3} = 4\pi + \dfrac{\pi }{3}\)
Vì M và N lệch pha nhau một góc\(\Delta \varphi = 4\pi + \dfrac{\pi }{3}\) và M dao động nhanh pha hơn nên tại thời điểm t N ở vị trí thấp nhất thì điểm M và N được biểu diễn trên VTLG như sau:
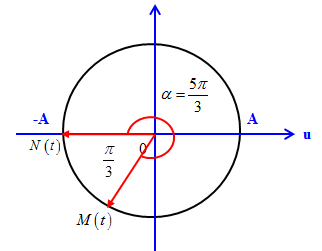
Để điểm M đi đến vị trí thấp nhất thì nó phải quay thêm góc: \(\alpha = \dfrac{{5\pi }}{3}rad\)
→ Thời gian quay là: \(\Delta t = \dfrac{\alpha }{\omega } = \dfrac{{\dfrac{{5\pi }}{3}}}{{2\pi .10}} = \dfrac{1}{{12}}s\)
Chọn D.










