Một vật dao động điều hoà với phương trình liên hệ giữa li độ x và vận tốc v là v^2 = 640 - 40x^2 tr

Câu hỏi
Nhận biếtMột vật dao động điều hoà với phương trình liên hệ giữa li độ x và vận tốc v là \({v^2} = 640 - 40{x^2}\), trong đó x tính bằng cm và v tính bằng cm/s. Tại thời điểm \(t = \dfrac{{67}}{{12}}\,\,s\), vật qua vị trí cân bằng theo chiều âm. Lấy \({\pi ^2} = 10\). Phương trình dao động của vật là?
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Ta có: \({v^2} = 640 - 40{x^2} \Rightarrow 40{x^2} + {v^2} = 640 \Rightarrow {x^2} + \dfrac{{{v^2}}}{{40}} = 16\)
Từ công thức độc lập với thời gian, ta có:
\(\left\{ \begin{array}{l}{\omega ^2} = 40 \Rightarrow \omega = 2\pi \,\,\left( {rad/s} \right)\\{A^2} = 16 \Rightarrow A = 4\,\,\left( {cm} \right)\end{array} \right.\)
Tại thời điểm \(t = \dfrac{{67}}{{12}}\,\,s\), vecto quay được góc: \(\Delta \varphi = \omega t = 2\pi .\dfrac{{67}}{{12}} = \dfrac{{67\pi }}{6} = 10\pi + \dfrac{{7\pi }}{6}\,\,\left( {rad} \right)\)
Ta có vòng tròn lượng giác:
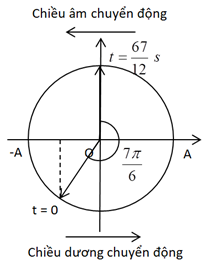
Từ vòng tròn lượng giác, ta thấy ở thời điểm t, pha dao động của vật là: \({\varphi _t} = \dfrac{\pi }{2}\)
Pha ban đầu của dao động là: \(\varphi = {\varphi _t} - \Delta \varphi = \dfrac{\pi }{2} - \dfrac{{7\pi }}{6} = - \dfrac{{2\pi }}{3}\,\,\left( {rad} \right)\)
Vậy phương trình dao động của vật là: \(x = 4\cos \left( {2\pi t - \dfrac{{2\pi }}{3}} \right)\,\,\left( {cm} \right)\)
Chọn C.










