Một nguồn phát sóng dao động điều hòa tạo ra sóng tròn đồng tâm O truyền trên mặt nước với bước sóng

Câu hỏi
Nhận biếtMột nguồn phát sóng dao động điều hòa tạo ra sóng tròn đồng tâm O truyền trên mặt nước với bước sóng l. Hai điểm M và N thuộc mặt nước, nằm trên hai phương truyền sóng mà các phần tử nước đang dao động. Biết OM = 8\(\text{ }\!\!\lambda\!\!\text{ }\), ON = 12\(\text{ }\!\!\lambda\!\!\text{ }\) và OM vuông góc với ON. Trên đoạn MN, số điểm mà phần tử nước dao động ngược pha với dao động của nguồn O là
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Ta có: \(\frac{1}{O{{H}^{2}}}=\frac{1}{O{{M}^{2}}}+\frac{1}{O{{N}^{2}}}=\frac{1}{{{\left( 8\lambda \right)}^{2}}}+\frac{1}{{{\left( 12\lambda \right)}^{2}}}\Rightarrow OH=6,66\lambda \)Các điểm dao động ngược pha với O cách O một khoảng \(d=\frac{2k+1}{2}\lambda \)
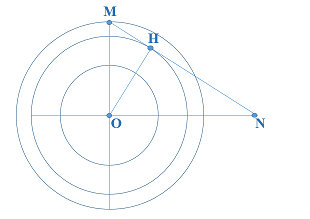
Số điểm nằm trên MH : \(6,66\lambda \le \frac{2k+1}{2}\lambda \le 8\lambda \Rightarrow 6,16\le k\le 7,5\Rightarrow k=7\), có 1 điểm
Số điểm nằm trên NH : \(6,66\lambda \le \frac{2k+1}{2}\lambda \le 12\lambda \Rightarrow 6,16\le k\le 11,5\Rightarrow k=7,8,9,10,11\), có 5 điểm
Tổng số điểm dao động ngược pha với O là: 6
Chọn C










