Đặt điện áp xoay chiều có giá trị hiệu dụng không đổi vào hai đầu đoạn mạch AB. Hình bên gồm đoạn mạ
Câu hỏi
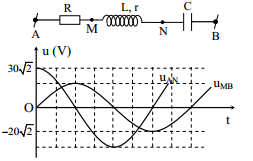
Nhận biếtĐặt điện áp xoay chiều có giá trị hiệu dụng không đổi vào hai đầu đoạn mạch AB. Hình bên gồm đoạn mạch AB và đồ thị biểu diễn điện áp uAN và uMB phụ thuộc vào thời gian t. Biết công suất tiêu thụ trên đoạn AM bằng công suất tiêu thụ trên đoạn MN. Giá trị của U gần nhất với giá trị nào sau đây?
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
Từ đồ thị ta thấy uAN sớm pha π/2 so với uMB và UAN= 30V; UMB= 20V
Vì PAM = PMN => R = r
Vì uAN sớm pha π/2 so với uMB nên ta có:
\(\tan {{\varphi }_{AN}}.\tan {{\varphi }_{MB}}=-1\Rightarrow \frac{{{Z}_{L}}}{R+r}.\frac{{{Z}_{C}}-{{Z}_{L}}}{r}=1\Rightarrow {{Z}_{C}}-{{Z}_{L}}=\frac{2{{R}^{2}}}{{{Z}_{L}}}\)
Mặt khác:
\(\frac{U_{AN}^{2}}{U_{MB}^{2}}=\frac{Z_{AN}^{2}}{Z_{MB}^{2}}=\frac{{{(R+r)}^{2}}+Z_{L}^{2}}{{{r}^{2}}+{{({{Z}_{C}}-{{Z}_{L}})}^{2}}}=\frac{9}{4}\Rightarrow \frac{4{{R}^{2}}+Z_{L}^{2}}{{{R}^{2}}+{{({{Z}_{C}}-{{Z}_{L}})}^{2}}}=\frac{9}{4}\)
\(\Rightarrow 16{{R}^{2}}+4Z_{L}^{2}=9{{R}^{2}}+9{{({{Z}_{C}}-{{Z}_{L}})}^{2}}\Rightarrow 7{{R}^{2}}+4Z_{L}^{2}=9.\frac{4{{R}^{4}}}{Z_{L}^{2}}\Rightarrow 4Z_{L}^{4}+7{{R}^{2}}Z_{L}^{2}-36{{R}^{4}}=0\Rightarrow {{Z}_{L}}=1,5R\Rightarrow {{Z}_{C}}=\frac{17R}{6}\) Ta có: \(\frac{{{U}_{AN}}}{{{U}_{AB}}}=\frac{{{Z}_{AN}}}{{{Z}_{AB}}}=\frac{\sqrt{4{{R}^{2}}+Z_{L}^{2}}}{\sqrt{4{{R}^{2}}+{{({{Z}_{C}}-{{Z}_{L}})}^{2}}}}=1,04\Rightarrow {{U}_{AB}}=29V\)
Chọn C
