Một con lắc lò xo dao động điều hòa theo phương thẳng đứng gốc O ở VTCB. Tại các thời điểm t1; t2; t

Câu hỏi
Nhận biếtMột con lắc lò xo dao động điều hòa theo phương thẳng đứng, gốc O ở VTCB. Tại các thời điểm t1; t2; t3 lò xo dãn a (cm); 2a (cm); 3a (cm) tương ứng với tốc độ của vật là \(v\sqrt{8}\) (cm/s); \(v\sqrt{6}\) (cm/s) và \(v\sqrt{2}\) (cm/s). Tỉ số giữa thời gian lò xo nén và lò xo dãn trong 1 chu kỳ là
Đáp án đúng: B
Lời giải của Tự Học 365
Giải chi tiết:
Giả sử ở VTCB lò xo dãn Δl
Áp dụng hệ thức độc lập ta được:
\({{A}^{2}}={{(a-\Delta l)}^{2}}+\frac{8{{v}^{2}}}{{{\omega }^{2}}}\)
\({{A}^{2}}={{(2a-\Delta l)}^{2}}+\frac{6{{v}^{2}}}{{{\omega }^{2}}}\)
\({{A}^{2}}={{(3a-\Delta l)}^{2}}+\frac{2{{v}^{2}}}{{{\omega }^{2}}}\)
Từ 3 phương trình trên ta được a = 2Δl \(\Rightarrow A=\sqrt{33}\Delta l\)
Biểu diễn vị trí lò xo nén (-Δl; -A) và lò xo dãn (-Δl ; A)
\(\cos \varphi =\frac{\Delta l}{A}=\frac{1}{\sqrt{33}}\Rightarrow \varphi ={{80}^{0}}\)
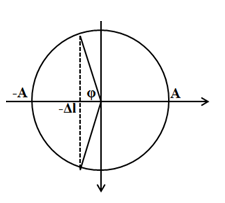
Tỉ số thời gian lò xo nén và dãn trong 1 chu kỳ là
\(\frac{{{t}_{nen}}}{{{t}_{dan}}}=\frac{160}{200}=0,8\)
Chọn B










