Đoạn áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu đoạn mạch gồm biến trở cuộn

Câu hỏi
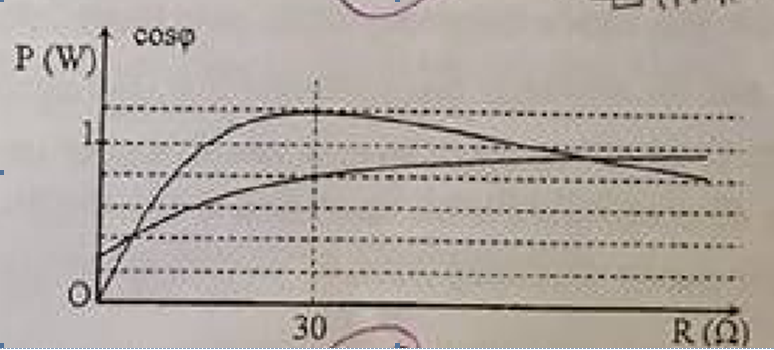
Nhận biếtĐoạn áp xoay chiều có giá trị hiệu dụng và tần số không đổi vào hai đầu đoạn mạch gồm biến trở, cuộn dây và tụ điện mắc nối tiếp. Hình vẽ bên là đồ thị biểu diễn sự phụ thuộc của công suất tỏa nhiệt P trên biến trở và hệ số công suất cosφ của đoạn mạch theo giá trị R của biến trở. Điện trở của cuả cuộn dây có giá trị gần nhất với giá trị nào sao đây?
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Từ hình vẽ ta có thấy tại R = 30Ω, thì công suất đoạn mạch là 0,8 và công suất tiêu thụ trên biến trở là cực đại
Ta có:
\(\begin{array}{l}
\cos \varphi = \frac{{R + r}}{Z} = 0,8 \Leftrightarrow R + r = 0,8Z \Leftrightarrow {(R + r)^2} = 0,64\left[ {{{(R + r)}^2} + {{({Z_L} - {Z_C})}^2}} \right]\\
\Leftrightarrow 0,36{(R + r)^2} = 0,64{({Z_L} - {Z_C})^2}\\
\Leftrightarrow 0,6.(R + r) = 0,8.({Z_L} - {Z_C})\\
{P_R} = {I^2}.R = \frac{{{U^2}}}{{\left[ {{{(R + r)}^2} + {{({Z_L} - {Z_C})}^2}} \right]}}.R = \frac{{{U^2}}}{{\frac{1}{R}.({R^2} + 2Rr + {r^2} + {{({Z_L} - {Z_C})}^2})}} = \frac{{{U^2}}}{{R + 2r + \frac{{{r^2} + {{({Z_L} - {Z_C})}^2}}}{R}}} = \frac{{{U^2}}}{y}\\
{\mathop{\rm cosi}\nolimits} :R + \frac{{{r^2} + {{({Z_L} - {Z_C})}^2}}}{R} \ge 2.\sqrt {{r^2} + {{({Z_L} - {Z_C})}^2}} \\
y = R + 2r + \frac{{{r^2} + {{({Z_L} - {Z_C})}^2}}}{R} \ge 2r + (2.\sqrt {{r^2} + {{({Z_L} - {Z_C})}^2}} )\\
= > {P_{R\max }} = \frac{{{U^2}}}{{2r + (2.\sqrt {{r^2} + {{({Z_L} - {Z_C})}^2}} )}} \Leftrightarrow R = \frac{{{r^2} + {{({Z_L} - {Z_C})}^2}}}{R} \Leftrightarrow {R^2} = {r^2} + {({Z_L} - {Z_C})^2}\\
{R^2} = {r^2} + {({Z_L} - {Z_C})^2} = {r^2} + \frac{{0,36}}{{0,64}}.{(R + r)^2}\\
\Leftrightarrow {R^2} = {r^2} + 0,5625.({R^2} + 2Rr + {r^2})\\
\Leftrightarrow 1,5625{r^2} + 1,125Rr - 0,4375{R^2} = 0\\
\Leftrightarrow 1,5625{r^2} + 33,75r - 393,75 = 0\\
\Leftrightarrow \left[ \begin{array}{l}
{r_1} = 8,4\Omega \\
{r_2} = - 30\Omega
\end{array} \right.
\end{array}\)
chọn đáp án r = 8,4Ω
Vậy đáp án gần nhất với giá trị r là đáp án D.