[LỜI GIẢI] Với abc là các số thực dương thỏa mãn ab + bc + ca = 3abc. Tìm giá trị nhỏ nhất của P = < - Tự Học 365
LUYỆN TẬP TRẮC NGHIỆM 50000+ CÂU HỎI

DÀNH CHO MỌI LỚP 6 ĐẾN 12

TRUY CẬP NGAY
XEM CHI TIẾT

Với abc là các số thực dương thỏa mãn ab + bc + ca = 3abc. Tìm giá trị nhỏ nhất của P = <

Với abc là các số thực dương thỏa mãn ab + bc + ca = 3abc. Tìm giá trị nhỏ nhất của P = <

Câu hỏi

Nhận biết

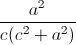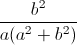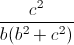
Với a,b,c là các số thực dương thỏa mãn ab + bc + ca = 3abc. Tìm giá trị nhỏ nhất của P = \frac{a^{2}}{c(c^{2}+a^{2})} + \frac{b^{2}}{a(a^{2}+b^{2})} + \frac{c^{2}}{b(b^{2}+c^{2})}


Đáp án đúng: A

Lời giải của Tự Học 365

Giải chi tiết:

Ta có = -

= - ≥ -

Tương tự ≥ - ≥ -

Từ đó P ≥ ( + + ) = = .

Dấu “=” xảy ra khi và chỉ khi a = b = c = 1

Vậy Pmin = 3/2.

Ý kiến của bạn

Luyện tập

Câu hỏi liên quan

  • câu 7 

    câu 7 

    Chi tiết
  • câu 2 

    câu 2 

    Chi tiết
  • Câu 2: Đề thi thử THPT Hà Trung - Thanh Hóa

    Câu 2: Đề thi thử THPT Hà Trung - Thanh Hóa

    Chi tiết
  • Giải phương trình 3<sup>1 – x</sup> – 3<sup>x</sup> + 2 = 0.

    Giải phương trình 31 – x – 3x + 2 = 0.

    Chi tiết
  • Giải phương trình : z<sup>3</sup> + i = 0

    Giải phương trình : z3 + i = 0

    Chi tiết
  • Giải phương trình (1 – i)z + (2 – i) = 4 – 5i trên tập số ph

    Giải phương trình (1 – i)z + (2 – i) = 4 – 5i trên tập số phức. 

    Chi tiết
  • Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y

    Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d: = = và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình  mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.

    Chi tiết
  • Tìm số nguyên dương n nhỏ nhất sao cho z<sub>1 </sub>=

    Tìm số nguyên dương n nhỏ nhất sao cho z1 = là số thực và z2 = là số ảo.

    Chi tiết
  • Giải phương trình: (sin2x + cos2x)cosx + 2cos2x - sinx = 0

    Giải phương trình: (sin2x + cos2x)cosx + 2cos2x - sinx = 0

    Chi tiết
  • Giải phương trình 7<sup>2x + 1</sup> – 8.7<sup>x</sup> + 1 =

    Giải phương trình 72x + 1 – 8.7x + 1 = 0.

    Chi tiết