Giải phương trình (1 – i)z + (2 – i) = 4 – 5i trên tập số ph

Câu hỏi
Nhận biếtGiải phương trình (1 – i)z + (2 – i) = 4 – 5i trên tập số phức.
Đáp án đúng: C
Lời giải của Tự Học 365
Lời giải chi tiết:
Phương trình đã cho tương đương với phương trình (1 – i)z = 2 – 4i ⇔z = 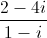
⇔z =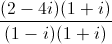
⇔z = 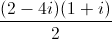
⇔z = 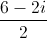
⇔z = 3 – i.
Vậy nghiệm của phương trình là z = 3 – i.


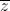 =
= 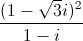 . Tìm modun của số phức
. Tìm modun của số phức  là số thực và z2 =
là số thực và z2 =  là số ảo.
là số ảo.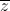 = (
= (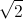 + i)2 (1 -
+ i)2 (1 -