Trong mặt phẳng với hệ tọa độ Oxy cho hình thoi ABCD có phương trình đường thẳng AC là x + 7y - 31 =
Câu hỏi
Nhận biếtTrong mặt phẳng với hệ tọa độ Oxy, cho hình thoi ABCD có phương trình đường thẳng AC là x + 7y - 31 = 0, hai đỉnh B, D lần lượt thuộc các đường thẳng d1: x + y - 8 = 0, d2: x - 2y + 3 = 0. Tìm tọa độ các đỉnh của hình thoi biết rằng diện tích hình thoi bằng 75 và đỉnh A có hoành độ âm .
Đáp án đúng: C
Lời giải của Tự Học 365
Giải chi tiết:
B ∈ d1: y = 8 - x => B(b; 8 – b),
D ∈ d2: x = 2y - 3 => D(2d - 3; d),
=> 
= (-b + 2d - 3; b + d - 8) và trung điểm BD là
I (
)
Theo tính chất hình thoi => BD ⊥ AC
<=> 
. = 0 <=> -8b + 13d - 13 = 0 (*)
Do I là trung điểm của BD nên theo tính chất hình thoi, I là trung điểm của AC
Thay tọa độ điểm I vào AC ta có phương trình: -6b + 9d - 9 = 0 (**)
Kết hợp giữa (*) và (**) ta được b = 0; d = 1
Suy ra B(0; 8); D(-1; 1) => I(
).
A ∈ AC: x = -7y + 31 => A(-7a + 31; a)
SABCD = 
.AC.BD => AC = 
= 15√2 => IA =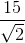 
=>(-7a + 
)2 + (a - 
)2 = 
⇔ (a - )2 = 
⇔ a = 3 hoặc a = 6
Với a = 3 => A(10; 3)
Với a = 6 => A(-11; 6) (không thỏa mãn)
Suy ra A(10; 3) => C(-11; 6) .
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
