Trong kì thi tuyển sinh đại học bạn An dự thi hai môn thi trắc nghiệm Vật lí và Hóa học đề thi của m
Câu hỏi
Nhận biếtTrong kì thi tuyển sinh đại học, bạn An dự thi hai môn thi trắc nghiệm Vật lí và Hóa học, đề thi của mỗi môn gồm 50 câu hỏi, mỗi câu có 4 phương án lựa chọn, trả lời đúng mỗi câu được 0,2 điểm. Mỗi môn thi An đều trả lời hết các câu hỏi và chắc chắn đúng 45 câu; 5 câu còn lại An chọn ngẫu nhiên. Tính xác suất để tổng số điểm 2 môn thi của An không dưới 19 điểm.
Đáp án đúng: D
Lời giải của Tự Học 365
Giải chi tiết:
Bạn An được không dưới 19 điểm khi và chỉ khi trong mười câu trả lời ngẫu nhiên ở hai môn thi trắc nghiệm Vật lí và Hóa học, bạn An trả lời đúng ít nhất 5 câu.
Xác suất trả lời đúng một câu hỏi là 
, trả lời sai là 
. Ta có
Xác suất trả lời đúng 5 trên 10 câu là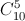 
.
;
Xác suất trả lời đúng 6 trên 10 câu là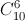 
.
;
Xác suất trả lời đúng 7 trên 10 câu là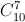 
.
;
Xác suất trả lời đúng 8 trên 10 câu là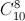 
. 
;
Xác suất trả lời đúng 9 trên 10 câu là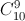 
. ;
Xác suất trả lời cả 10 câu là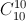 
.
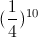Cộng các xác suất trên ta suy ra xác suất An được không dưới 19 điểm là 0,0781.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
