Trong không gian với hệ tọa độ Oxyz xét mặt cầu ( S ) đi qua hai điểm A( 1;6;2 )B( 3;0;0 ) và có tâ
Câu hỏi
Nhận biếtTrong không gian với hệ tọa độ \(Oxyz\), xét mặt cầu \(\left( S \right)\) đi qua hai điểm \(A\left( 1;6;2 \right),B\left( 3;0;0 \right)\) và có tâm thuộc mặt phẳng \(\left( P \right):x-y+2=0\). Bán kính mặt cầu \(\left( S \right)\) có giá trị nhỏ nhất là
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Cách 1. Gọi \(I\left( a;b;c \right)\) là tâm của mặt cầu \(\left( S \right),\) vì \(I\in \left( S \right)\)\(\Rightarrow I\left( a;a+2;c \right).\)
Ta có \(R=IA=IB\Leftrightarrow {{\left( a-1 \right)}^{2}}+{{\left( a-4 \right)}^{2}}+{{\left( c-2 \right)}^{2}}={{\left( a-3 \right)}^{2}}+{{\left( a+2 \right)}^{2}}+{{c}^{2}}\Leftrightarrow c=2-2a.\)
Khi đó \(R=IA=\sqrt{{{\left( a-1 \right)}^{2}}+{{\left( a-4 \right)}^{2}}+4{{a}^{2}}}=\sqrt{6{{a}^{2}}-10a+17}=\sqrt{6{{\left( x-\frac{5}{6} \right)}^{2}}+\frac{77}{6}}\ge \frac{\sqrt{462}}{6}.\)
Vậy bán kính nhỏ nhất của mặt cầu \(\left( S \right)\) là \({{R}_{\min }}=\frac{\sqrt{462}}{6}.\)
Cách 2. Tham khảo hình vẽ bên.
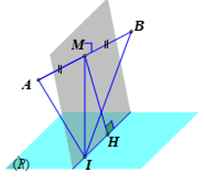
Ta có I thuộc giao tuyến mặt phẳng trung trực AB và \(\left( P \right)\)\(\Rightarrow IM\ge MH.\)
\(\Rightarrow R\ge HA\Rightarrow {{R}_{\min }}=HA\) với H là hình chiếu của M trên giao tuyến \(\Rightarrow \) \({{R}_{\min }}=\frac{\sqrt{462}}{6}.\)
Chọn A
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.