Trong không gian với hệ tọa độ Oxyz, cho hai điểm A( 3;-2;6 ),,,B( 0;1
Câu hỏi
Nhận biếtTrong không gian với hệ tọa độ Oxyz, cho hai điểm \(A \left( 3;-2;6 \right), \, \,B \left( 0;1;0 \right) \) và mặt cầu \( \left( S \right): \, \,{{ \left( x-1 \right)}^{2}}+{{ \left( y-2 \right)}^{2}}+{{ \left( z-3 \right)}^{2}}=25 \). Mặt phẳng \( \left( P \right): \, \,ax+by+cz-2=0 \) đi qua A, B và cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính \(T=a+b+c. \)
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
\(\begin{align} & B\in \left( P \right)\Rightarrow b-2=0\Leftrightarrow b=2 \\ & A\in \left( P \right)\Rightarrow 3a-2b+6c-2=0\Rightarrow a+2c=2\Rightarrow a=2-2c \\\end{align}\)
Khi đó mặt phẳng (P) có dạng : \(\left( P \right):\,\,\left( 2-2c \right)x+2y+cz-2=0\)
Mặt cầu \(\left( S \right)\) có tâm \(I\left( 1;2;3 \right)\), bán kính \(R=5\).
Gọi H và K lần lượt là chân đường vuông góc của I trên (P) và trên đường thẳng AB. Ta có : \(IH\le IK\)
Để mặt phẳng (P) cắt (S) theo giao tuyến là đường tròn có bán kính nhỏ nhất thì \(d{{\left( I;\left( P \right) \right)}_{\max }}=I{{H}_{\max }}=IK\Leftrightarrow H\equiv K.\)
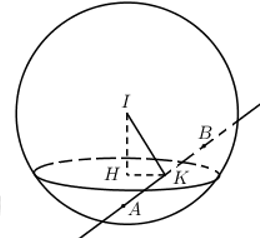
Ta có : \(\overrightarrow{AB}=\left( -3;3;-6 \right)=-3\left( 1;-1;2 \right)\)
\(\Rightarrow \) Phương trình đường thẳng AB : \(\left\{ \begin{align} & x=t \\ & y=1-t \\ & z=2t \\ \end{align} \right.,\,\,K\in AB\Rightarrow K\left( t;1-t;2t \right)\Rightarrow \overrightarrow{IK}=\left( t-1;-t-1;2t-3 \right)\)
Vì \(IK\bot AB\Rightarrow \overrightarrow{IK}.\overrightarrow{AB}=0\Rightarrow \left( t-1 \right)-\left( -t-1 \right)+2\left( 2t-3 \right)=0\Leftrightarrow 6t-6=0\Leftrightarrow t=1\Rightarrow K\left( 1;0;2 \right)\)
\(d{{\left( I;\left( P \right) \right)}_{\max }}=I{{H}_{\max }}=IK\Leftrightarrow H\equiv K\Rightarrow H\left( 1;0;2 \right)\Rightarrow \overrightarrow{IH}=\left( 0;-2;-1 \right)\) là 1 VTPT của (P).
\(\Rightarrow \overrightarrow{IH}\) và vector pháp tuyến \({{\overrightarrow{n}}_{\left( P \right)}}\,\left( 2-2c;2;c \right)\) cùng phương
\(\begin{array}{l}
\Rightarrow {\overrightarrow n _{\left( P \right)}} = k\overrightarrow {IH} \Rightarrow \left\{ \begin{array}{l}
2 - 2c = 0\\
2 = - 2k\\
c = - k
\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}
c = 1\\
k = - 1
\end{array} \right. \Rightarrow a = 2 - 2c = 0\\
\Rightarrow T = a + b + c = 0 + 2 + 1 = 3
\end{array}\)
Chọn A.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.
