Trong không gian Oxyz cho điểm A(1;-6;1) và mặt phẳng (P):x+y+7=0. Điểm B thay đổi thuộc Oz; điểm C
Câu hỏi
Nhận biếtTrong không gian Oxyz, cho điểm \(A(1;-6;1)\) và mặt phẳng \((P):x+y+7=0\). Điểm B thay đổi thuộc Oz; điểm C thay đổi thuộc mặt phẳng (P). Biết rằng tam giác ABC có chu vi nhỏ nhất. Tọa độ điểm B là
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
Nhận xét:
Ta dễ dàng kiểm tra được:
+) Oz song song với mặt phẳng \((P):x+y+7=0\)
+) Điểm \(A(1;-6;1)\) không thuộc đường thẳng \(Oz\) và mặt phẳng (P)
+) A và Oz nằm cùng phía so với mặt phẳng (P).
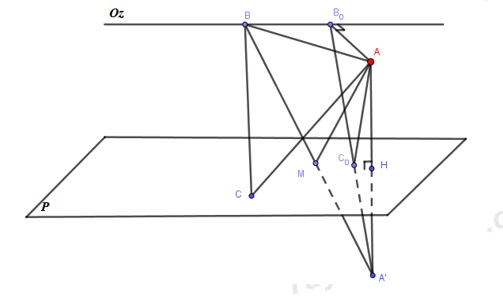
Gọi \({{B}_{0}},\,H\)lần lượt là hình chiếu của A lên Oz, (P).
A’ là điểm đối xứng của A qua (P).
Lấy \(B\in Oz,\,\,\,C\in (P)\)bất kì. Khi đó, ta chứng minh: \({{C}_{A{{B}_{0}}{{C}_{0}}}}\le {{C}_{ABC}}\)
Ta có:
\({{C}_{ABC}}=AB+(BC+AC)=AB+\left( BC+CA' \right)\) (vì (P) là mặt phẳng trung trực của đoạn thẳng AA’)
\(\ge A{{B}_{0}}+A'B\) ( Vì \(A{{B}_{0}}\bot Oz\))
\(\ge A{{B}_{0}}+A'{{B}_{0}}\) (Vì \(A'{{B}_{0}}\bot Oz\) (*) )
\(\begin{array}{l}= A{B_0} + A'{C_0} + {C_0}{B_0}\\ = A{B_0} + A{C_0} + {C_0}{B_0}\\ = {C_{A{B_0}{C_0}}}\end{array}\)
(Chứng minh (*) : Ta có: \(Oz//(P),\,\,AA'\bot (P)\Rightarrow Oz\bot AA'\) . Mà \(Oz\bot A{{B}_{0}}\Rightarrow Oz\bot (A{{B}_{0}}A')\Rightarrow Oz\bot A'{{B}_{0}}\))
Vậy, khi B, C lần lượt trùng với các điểm \({{B}_{0}},\,{{C}_{0}}\) xác định như trên, chu vi tam giác ABC là nhỏ nhất.
* Tìm tọa độ điểm \({{B}_{0}}\)?
Tọa độ hình chiếu của \(A(1;-6;1)\) lên Oz là: (0; 0; 1)
Vậy, \({{B}_{0}}(0;0;1)\).
Chọn: A.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.