Trên cánh đồng có 2 con bò được cột vào 2 cây cọc khác nhau. Biết khoảng cách giữa hai cọc là 4 mét
Câu hỏi
Nhận biếtTrên cánh đồng có \(2\) con bò được cột vào \(2\) cây cọc khác nhau. Biết khoảng cách giữa hai cọc là \(4\) mét, còn \(2\) sợi dây cột \(2\) con bò dài \(3\) mét và \(2\) mét. Tính phần diện tích mặt cỏ lớn nhất mà \(2\) con bò có thể ăn chung (lấy giá trị gần đúng nhất).
Đáp án đúng: A
Lời giải của Tự Học 365
Giải chi tiết:
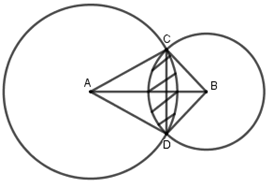
Con bò thứ nhất có thể ăn cỏ trong hình tròn tâm \(A\) bán kính \(AC = 3m\).
Con bò thứ hai có thể ăn cỏ trong hình tròn tâm \(B\) bán kính \(BC = 2m\).
Phần diện tích lớn nhất hai con có thể ăn chung là phần giao của hai hình tròn (phần gạch sọc).
Xét tam giác \(ABC\) có \(AC = 3,BC = 2,AB = 4\) \( \Rightarrow \cos \angle ABC = \frac{{B{A^2} + B{C^2} - A{C^2}}}{{2BA.BC}} = \frac{{11}}{{16}}\)
\(\begin{array}{l} \Rightarrow \angle ABC \approx {46^0}34' \Rightarrow \angle CBD \approx {93^0}8' \Rightarrow {S_{qCBD}} = \frac{{{{93}^0}8'.\pi B{C^2}}}{{{{360}^0}}} \approx 3,251{m^2}\\ \Rightarrow \cos \angle CAB = \frac{{A{C^2} + A{B^2} - B{C^2}}}{{2AC.AB}} = \frac{7}{8} \Rightarrow \angle CAB \approx {28^0}57' \Rightarrow \angle CAD \approx {57^0}54'\\ \Rightarrow {S_{qCAD}} = \frac{{{{57}^0}54'.\pi A{C^2}}}{{{{360}^0}}} \approx 4,548{m^2}\end{array}\)
Lại có \({S_{\Delta CBD}} = \frac{1}{2}BC.BD.\sin \angle CBD \approx 1,997{m^2}\) và \({S_{\Delta CAD}} = \frac{1}{2}AC.AD.\sin \angle CAD \approx 3,812{m^2}\).
Vậy \(S = \left( {{S_{qCAD}} - {S_{\Delta CAD}}} \right) + \left( {{S_{qCBD}} - {S_{\Delta CBD}}} \right) = \left( {4,548 - 3,812} \right) + \left( {3,251 - 1,997} \right) = 1,99{m^2}\)
Chọn A.
Luyện tập
Câu hỏi liên quan
-
Trong không gian với hệ trục Oxyz, cho mặt phẳng (P): 2x + y + 2z + 4 = 0, đường thẳng d:
= 
= 
và đường thẳng ∆ là giao tuyến của hai mặt phẳng x = 1, y + z - 4 = 0. Viết phương trình mặt cầu có tâm thuộc d, đồng thời tiếp xúc với ∆ và (P) biết rằng tâm của mặt cầu có tọa độ nguyên.
là số thực và z2 = 
là số ảo.